
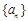 的前n项和为
的前n项和为  (n∈N*),且
(n∈N*),且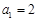 .数列
.数列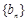 满足
满足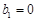 ,
,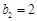 ,
,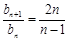 ,n=2,3,….
,n=2,3,….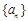 的通项公式;
的通项公式;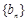 的通项公式;
的通项公式;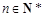 ,
,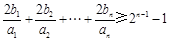 .
.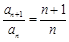 . …………… 2分
. …………… 2分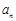 =
=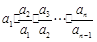 =
=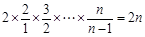 .
.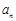 =2n(n∈N*). …………………………………… 4分
=2n(n∈N*). …………………………………… 4分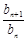 =
=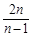 (n≥2),b
(n≥2),b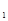 =0,b
=0,b =2,
=2,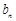 =b
=b

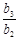

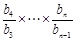 =2
=2
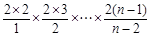 ,
,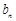 =
=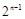 (n-1)(n≥3). ……………………………………………… 8分
(n-1)(n≥3). ……………………………………………… 8分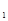 =0,b
=0,b =2 满足上式,
=2 满足上式,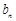 } 的通项公式为
} 的通项公式为 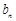 =
=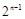 (n-1). …………………………………… 10分
(n-1). …………………………………… 10分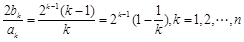
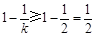 .
.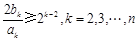 …………………………………………………… 11分
…………………………………………………… 11分 (n∈N*).… 12分
(n∈N*).… 12分

科目:高中数学 来源:不详 题型:解答题
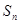 是数列
是数列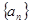 的前
的前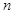 项和,
项和,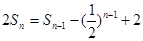 (
(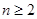 ,
,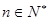 ),且
),且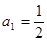 .
.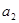 的值,并写出
的值,并写出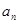 和
和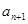 的关系式;
的关系式;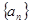 的通项公式及
的通项公式及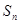 的表达式;
的表达式; 3)我们可以证明:若数列
3)我们可以证明:若数列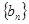 有上界(即存在常数
有上界(即存在常数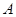 ,使得
,使得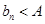 对一切
对一切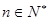 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列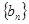 有下界(即存在常数
有下界(即存在常数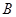 ,使得
,使得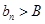 对一切
对一切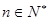 恒成立)且单调递减,则
恒成立)且单调递减,则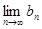 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: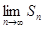 存在.
存在. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)

 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
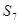 ,并归纳出
,并归纳出 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com