
科目:高中数学 来源: 题型:
某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可表示为( )
A.y=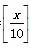 B.y=
B.y=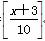
C.y=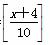 D.y=
D.y=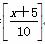
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)的定义域为A,若x1,x2∈A且f(x1)=f(x2)时总有x1=x2,则称f(x)为单函数.例如:函数f(x)=2x+1(x∈R)是单函数.
给出下列命题:
①函数f(x)=x2(x∈R)是单函数;
②指数函数f(x)=2x(x∈R)是单函数;
③若f(x)为单函数,x1,x2∈A且x1≠x2,则f(x1)≠f(x2);
④在定义域上具有单调性的函数一定是单函数.
其中真命题是________(写出所有真命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x+bcos x,其中b为常数.那么“b=0”是“f(x)为奇函数”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
在实数的原有运算法则中,我们补充定义新运算“⊕”:当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)的图象与x轴及直线x=2围成的面积为( )
A.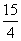 B.4 C.
B.4 C.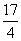 D.8
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com