
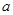 个红球,
个红球,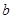 个黄球,
个黄球,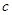 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,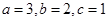 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求 分布列;
分布列;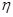 为取出此球所得分数.若
为取出此球所得分数.若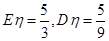 ,求
,求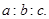
 | 2 | 3 | 4 | 5 | 6 |
| P | 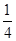 | 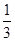 | 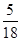 | 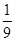 | 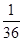 |
 的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量
的取值可能分别是2,3,4,5,6,即当两次摸到的球分别是红红时得2分,当两次摸到的球分别是红黄或黄红时得3分,当两次摸到的球分别是黄黄或红蓝或蓝红时得4分,当两次摸到的球分别是黄蓝或蓝黄时得5分,当两次摸到的球分别是蓝蓝时得6分;第(2)文关键是搞清楚随机变量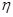 的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于
的取值有哪些,然后求出对应的概率,利用随机变量的期望和方差的计算公式列出关于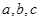 的方程即可求出他们关系;
的方程即可求出他们关系;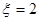 ,此时
,此时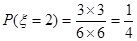 ;当两次摸到的球分别是黄黄,红蓝,蓝红时
;当两次摸到的球分别是黄黄,红蓝,蓝红时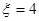 ,此时
,此时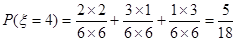 ;当两次摸到的球分别是红黄,黄红时
;当两次摸到的球分别是红黄,黄红时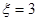 ,此时
,此时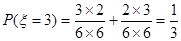 ;当两次摸到的球分别是黄蓝,蓝黄时
;当两次摸到的球分别是黄蓝,蓝黄时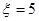 ,此时
,此时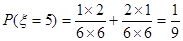 ;当两次摸到的球分别是蓝蓝时
;当两次摸到的球分别是蓝蓝时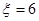 ,此时
,此时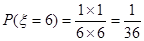 ;所以
;所以 的分布列是:
的分布列是: | 2 | 3 | 4 | 5 | 6 |
| P | 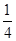 | 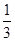 | 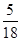 | 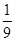 | 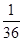 |
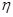 有三种取值即1,2,3,所以
有三种取值即1,2,3,所以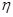 的分布列是:
的分布列是: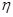 | 1 | 2 | 3 |
| P | 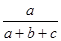 | 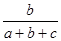 | 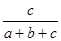 |
 ,所以
,所以
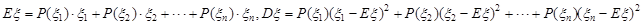 ;若服从正态分布,即
;若服从正态分布,即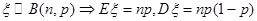 ;
;

科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立. 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,落在圆盘中2分处的概率为
,落在圆盘中2分处的概率为 ,落在圆盘中0分处的概率为
,落在圆盘中0分处的概率为 ,(
,( ),已知旋转一次圆盘得分的数学期望为1分,则
),已知旋转一次圆盘得分的数学期望为1分,则 的最小值为
的最小值为
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com