Question

5．已知正四棱台两底面边长分别为a和b（a＜b）．
（1）若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°，求棱台的侧面积；
（2）若棱台的侧面积等于两底面面积之和，求它的高．

Answer 1

分析 （1）如图所示，由于PO⊥平面ABCD，侧棱所在直线与上、下底面正方形中心的连线所成的角为45°，可得∠PAO=45°，PO=OA=$\frac{\sqrt{2}}{2}b$，PO₁=O₁A₁=$\frac{\sqrt{2}}{2}$a．分别取AB，A₁B₁的中点E，E₁，连接OE，O₁E₁．利用勾股定理可得：PE，PE₁．可得斜高EE₁=PE-PE₁．即可得出棱台的侧面积S_侧．
（2）由棱台的侧面积等于两底面面积之和，可得$4×\frac{1}{2}（a+b）×E{E}_{1}$=a²+b²，利用OO₁=$\sqrt{E{E}_{1}^{2}-（EO-{E}_{1}O）^{2}}$即可得出．

解答 解：（1）如图所示，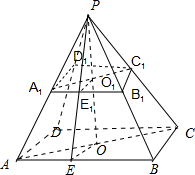
∵PO⊥平面ABCD，侧棱所在直线与上、下底面正方形中心的连线所成的角为45°，
∴∠PAO=45°，∴PO=OA=$\frac{\sqrt{2}}{2}b$，PO₁=O₁A₁=$\frac{\sqrt{2}}{2}$a．
分别取AB，A₁B₁的中点E，E₁，连接OE，O₁E₁．
则PE=$\sqrt{（\frac{b}{2}）^{2}+（\frac{\sqrt{2}}{2}b）^{2}}$=$\frac{\sqrt{3}}{2}b$，PE₁=$\sqrt{（\frac{a}{2}）^{2}+（\frac{\sqrt{2}}{2}a）^{2}}$=$\frac{\sqrt{3}}{2}a$．
∴斜高EE₁=PE-PE₁=$\frac{\sqrt{3}}{2}（b-a）$．
∴棱台的侧面积S_侧=$4×\frac{1}{2}（a+b）×\frac{\sqrt{3}}{2}（b-a）$=$\sqrt{3}（{b}^{2}-{a}^{2}）$；
（2）∵棱台的侧面积等于两底面面积之和，
∴$4×\frac{1}{2}（a+b）×E{E}_{1}$=a²+b²，
∴EE₁=$\frac{{a}^{2}+{b}^{2}}{2（a+b）}$．
∴OO₁=$\sqrt{E{E}_{1}^{2}-（EO-{E}_{1}O）^{2}}$=$\sqrt{[\frac{{a}^{2}+{b}^{2}}{2（a+b）}]^{2}-（\frac{b-a}{2}）^{2}}$=$\frac{ab}{a+b}$．

点评 本题考查了正四棱台的有关计算、直角三角形的边角关系、勾股定理、梯形的面积计算公式，考查了推理能力与计算能力，属于中档题．