Question

4．如图，在多面体ABCDE中，面ABED为梯形且∠BAD=∠EDA=$\frac{π}{2}$，F为CE的中点，AC=AD=CD=DE=AF=2，AB=1．
（1）求证：DF⊥BC；
（2）求平面BCE与平面ACD所成锐二面角的余弦值．

Answer 1

分析 （1）取CD的中点O，连接AO，FO，则AO⊥CD，证明AO⊥OF，可得AO⊥平面CDE，建立如图所示的坐标系，利用向量的方法证明DF⊥BC；
（2）确定平面BCE与平面ACD的法向量，即可求平面BCE与平面ACD所成锐二面角的余弦值．

解答 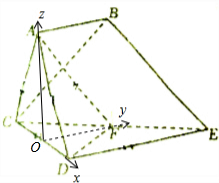（1）证明：取CD的中点O，连接AO，FO，则AO⊥CD
由题意，AO=$\sqrt{3}$，OF=1，
∵AF=2，
∴AO⊥OF，
∵CD∩OF=O，
∴AO⊥平面CDE，
建立如图所示的坐标系，则D（1，0，0），F（0，1，0），B（0，1，$\sqrt{3}$），C（-1，0，0），
∴$\overrightarrow{DF}$=（-1，1，0），$\overrightarrow{BC}$=（-1，-1，-$\sqrt{3}$），
∴$\overrightarrow{DF}•\overrightarrow{BC}$=0，
∴DF⊥BC；
（2）解：由（1）可得DF⊥平面CBE
∴平面CBE的法向量为$\overrightarrow{DF}$=（-1，1，0），
∵平面ACD的法向量为（0，1，0），
∴平面BCE与平面ACD所成锐二面角的余弦值为$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$．

点评 解决立体几何中的线、面的位置关系或度量关系，常用的方法是通过建立空间直角坐标系，转化为向量的问题来解决．