
【题目】设f(x)=x3-3ax2+2bx在x=1处有极小值-1.
(1)求a、b的值
(2)求出f(x)的单调区间;
(3)求f(x)的极大值.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】分析:(1)已知函数![]() 在
在![]() 处有极小值-1,即
处有极小值-1,即![]() ,所以先求导函数,再代入列方程组,即可解得
,所以先求导函数,再代入列方程组,即可解得![]() 的值
的值
(2)分别解不等式![]() 0和
0和![]() ,即可得函数
,即可得函数![]() 的单调增区间与单调递减区间
的单调增区间与单调递减区间
(3)由(2)可得函数![]() 的单调性,从而求出函数的极大值
的单调性,从而求出函数的极大值
详解:
(1) ![]() (x)=3x2-6ax+2b,由题意知
(x)=3x2-6ax+2b,由题意知
![]() 即
即![]() 解之得a=
解之得a=![]() ,b=-
,b=-![]()
(2)由(1)知f(x)=x3-x2-x,![]() (x)=3x2-2x-1=3(x+
(x)=3x2-2x-1=3(x+![]() )(x-1)
)(x-1)
当![]() (x)>0时,x>1或x<-
(x)>0时,x>1或x<-![]() ,
,
当![]() (x)<0时,-
(x)<0时,-![]() <x<1
<x<1
∴函数f(x)的单调增区间为(-∞,-![]() )和(1,+∞),减区间为(-
)和(1,+∞),减区间为(-![]() ,1)
,1)
(3)由(2)得到函数![]() 的单调性,可得
的单调性,可得![]() 的极大值=
的极大值=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面凸四边形![]() 中(凸四边形指没有角度数大于
中(凸四边形指没有角度数大于![]() 的四边形),
的四边形),![]() .
.

(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)已知![]() ,记四边形
,记四边形![]() 的面积为
的面积为![]() .
.
① 求![]() 的最大值;
的最大值;
② 若对于常数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.(直接写结果,不需要过程)
的取值范围.(直接写结果,不需要过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 中点,连接
中点,连接![]() ,则异面直线
,则异面直线![]() 和
和![]() 所成角的余弦值为_____.
所成角的余弦值为_____.

【答案】![]()
【解析】
连接CD1,CM,由四边形A1BCD1为平行四边形得A1B∥CD1,即∠CD1M为异面直线A1B和D1M所成角,再由已知求△CD1M的三边长,由余弦定理求解即可.
如图,

连接![]() ,由
,由![]() ,可得四边形
,可得四边形![]() 为平行四边形,
为平行四边形,
则![]() ,∴
,∴![]() 为异面直线
为异面直线![]() 和
和![]() 所成角,
所成角,
由正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 中点,
中点,
得![]() ,
,![]() .
.
在![]() 中,由余弦定理可得,
中,由余弦定理可得, .
.
∴异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
故答案为:![]() .
.
【点睛】
本题考查异面直线所成角的求法,异面直线所成的角常用方法有:将异面直线平移到同一平面中去,达到立体几何平面化的目的;或者建立坐标系,通过求直线的方向向量得到直线夹角或其补角.
【题型】填空题
【结束】
16
【题目】在![]() 中,角
中,角![]() 所对的边分别是
所对的边分别是![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 面积的最大值为_____.
面积的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为![]() ,半径为1,该纸片上的等边三角形
,半径为1,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() 、
、![]() 、
、![]() 为圆
为圆![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() 、
、![]() 、
、![]() 重合,得到三棱锥.当
重合,得到三棱锥.当![]() 的边长变化时,所得三棱锥体积的最大值为__________.
的边长变化时,所得三棱锥体积的最大值为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a3=9,a5=17,记数列 ![]() 的前n项和为Sn , 若
的前n项和为Sn , 若 ![]() ,对任意的n∈N*成立,则整数m的最小值为( )
,对任意的n∈N*成立,则整数m的最小值为( )
A.5
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在平面直角坐标系xOy中,圆C的方程为![]() ,且圆C与y轴交于M,N两点(点N在点M的上方),直线
,且圆C与y轴交于M,N两点(点N在点M的上方),直线![]() 与圆C交于A,B两点。
与圆C交于A,B两点。
(1)若![]() ,求实数k的值。
,求实数k的值。
(2)设直线AM,直线BN的斜率分别为![]() ,若存在常数
,若存在常数![]() 使得
使得![]() 恒成立?若存在,求出a的值.若不存在请说明理由。
恒成立?若存在,求出a的值.若不存在请说明理由。
(3)若直线AM与直线BN相较于点P,求证点P在一条定直线上。

查看答案和解析>>
科目:高中数学 来源: 题型:
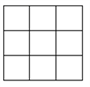
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com