
分析 (1)由已知求得b,把点的坐标代入椭圆方程求得a,则椭圆方程可求;
(2)假设存在实数m满足题设,联立直线方程与椭圆方程,由判别式大于0求得m的范围,再由根与系数的关系求得MN的中点P坐标,进一步求得PB的斜率结合|BM|=|BN|,可得BP⊥MN.由斜率的关系列式求得m值,说明不存在这样的实数m,使得|BM|=|BN|.
解答 解:(1)椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),过点$A(1,\frac{{\sqrt{6}}}{3})$和点B(0,-1),
∴b=1,由$\frac{1}{a^2}+\frac{{{{(\frac{{\sqrt{6}}}{3})}^2}}}{1}=1$,得a2=3.
∴椭圆G的方程为$\frac{x^2}{3}+{y^2}=1$;
(2)假设存在实数m满足题设,由$\left\{\begin{array}{l}y=x+m\\ \frac{x^2}{3}+{y^2}=1.\end{array}\right.$得4x2+6mx+3(m2-1)=0.
∵直线与椭圆有两个交点,∴△=36m2-48(m2-1)>0,即m2<4,…①
设MN的中点为P(xp,yp),xM,xN分别为点M,N的横坐标,
则${x_p}=\frac{{{x_M}+{x_N}}}{2}=-\frac{3m}{4}$,从而${y_p}={x_p}+m=\frac{m}{4}$,
∴${k_{BP}}=\frac{{{y_p}+1}}{x_p}=-\frac{m+4}{3m}$.
∵|BM|=|BN|,
∴BP⊥MN.
∴kBP•kMN=-1,而kMN=1.
∴$-\frac{m+4}{3m}=-1$,即m=2,与①矛盾.
因此,不存在这样的实数m,使得|BM|=|BN|.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,体现了“设而不求”的解题思想方法,是中档题.


科目:高中数学 来源: 题型:选择题
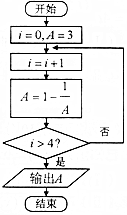 阅读如图的程序框图,运行相应的程序,输出的结果为( )
阅读如图的程序框图,运行相应的程序,输出的结果为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e0=1与ln 1=0 | B. | log39=2与9${\;}^{\frac{1}{2}}$=3 | ||
| C. | 8${\;}^{-\frac{1}{3}}$=$\frac{1}{2}$与log8$\frac{1}{2}$=-$\frac{1}{3}$ | D. | log77=1与71=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
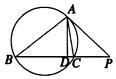 如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )
如图所示,PA切圆于A,PA=8,直线PCB交圆于C,B,连接AB,AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则$\frac{sinα}{sinβ}$的值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
数学 | 优 | 良 | 及格 | |
| 优 | 8 | m | 9 | |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com