
| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 每一次红球被摸到的概率P=$\frac{{∁}_{2}^{1}}{{∁}_{3}^{1}}$=$\frac{2}{3}$.由题意可得:X=0,1,2,3.X~B$(3,\frac{2}{3})$.即可得出.
解答 解:每一次红球被摸到的概率P=$\frac{{∁}_{2}^{1}}{{∁}_{3}^{1}}$=$\frac{2}{3}$.
由题意可得:X=0,1,2,3.X~B$(3,\frac{2}{3})$.
则D(X)=$3×\frac{2}{3}×(1-\frac{2}{3})$=$\frac{2}{3}$.
故选:C.
点评 本小题主要考查二项分布列的性质及其数学期望等基础知识,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$ | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | b>a>c | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
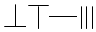 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )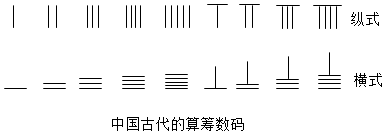
| A. | 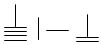 | B. | 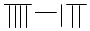 | C. |  | D. | 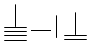 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
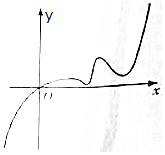 已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )
已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则$\frac{b+2}{a+2}$的取值范围是( )| A. | ($\frac{2}{3}$,2) | B. | (-∞,$\frac{2}{3}$)∪(2,+∞) | C. | (2,+∞) | D. | (-∞,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com