
(本小题满分12分)求函数 的最小正周期和最小值;
的最小正周期和最小值;
并写出该函数在 上的单调递增区间.
上的单调递增区间.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,在半径为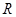 、圆心角为
、圆心角为 的扇形金属材料中剪出一个长方形
的扇形金属材料中剪出一个长方形 ,并且
,并且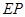 与
与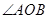 的平分线
的平分线 平行,设
平行,设 .
.
(1)试写出用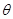 表示长方形
表示长方形 的面积
的面积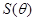 的函数;
的函数;
(2)在余下的边角料中在剪出两个圆(如图所示),试问当矩形 的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
的面积最大时,能否由这个矩形和两个圆组成一个有上下底面的圆柱?如果可能,求出此时圆柱的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且 求
求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,用半径为R的圆铁皮,剪一个圆心角为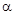 的扇形,制成一个圆锥形的漏斗,问圆心角
的扇形,制成一个圆锥形的漏斗,问圆心角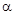 取什么值时,漏斗容积最大.(圆锥体积公式:
取什么值时,漏斗容积最大.(圆锥体积公式: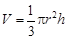 ,其中圆锥的底面半径为r,高为h)
,其中圆锥的底面半径为r,高为h)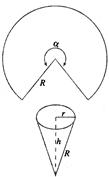
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com