
(本题满分12分)
是否存在常数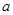 ,使得函数
,使得函数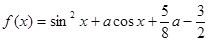 在闭区间
在闭区间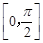 上的最大值为1?若存在,求出对应的
上的最大值为1?若存在,求出对应的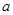 值;若不存在,说明理由.
值;若不存在,说明理由.
科目:高中数学 来源: 题型:解答题
燕子每年秋天都要从北方飞到南方过冬。研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数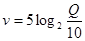 ,单位是
,单位是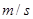 ,其中
,其中 表示燕子的耗氧量。
表示燕子的耗氧量。
(1)计算:两岁燕子静止时的耗氧量是多少个单位?(5分)
(2)当一只两岁燕子的耗氧量是80个单位时,它的飞行速度是多少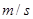 ?(5分)
?(5分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某商品在近30天内每天的销售价格P(元)与时间t(天)的函数关系式为:
P=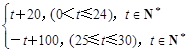 ;该商品的日销售量Q(件)与时间(天)的函数关系式为:
;该商品的日销售量Q(件)与时间(天)的函数关系式为:
Q=-t+40(0<t≤30,t∈N*).求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品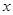 (百台),其总成本为
(百台),其总成本为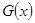 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为2万元(总成本=固定成本+生产成本).销售收入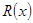 (万元)满足
(万元)满足 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出函数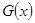 的解析式;
的解析式;
(2)写出利润函数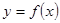 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
(3)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数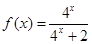 .
.
(Ⅰ)求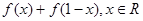 的值;
的值;
(Ⅱ)若数列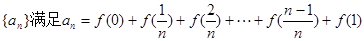
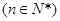 ,
,
求数列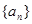 的通项公式;
的通项公式;
(Ⅲ)若数列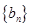 满足
满足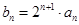 ,
,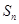 是数列
是数列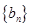 的前
的前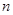 项和,是否存在正实数
项和,是否存在正实数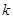 ,使不等式
,使不等式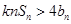 对于一切的
对于一切的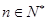 恒成立?若存在,请求出
恒成立?若存在,请求出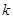 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某风景区有40辆自行车供游客租赁使用,管理这些自行车的费用是每日72元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com