
(本小题满分14分)
已知函数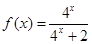 .
.
(Ⅰ)求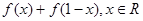 的值;
的值;
(Ⅱ)若数列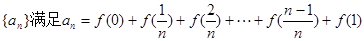
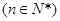 ,
,
求数列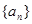 的通项公式;
的通项公式;
(Ⅲ)若数列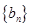 满足
满足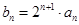 ,
,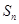 是数列
是数列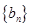 的前
的前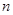 项和,是否存在正实数
项和,是否存在正实数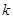 ,使不等式
,使不等式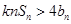 对于一切的
对于一切的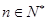 恒成立?若存在,请求出
恒成立?若存在,请求出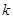 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(1)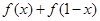 =1;(2)
=1;(2)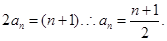 (3)
(3)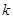
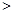
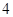 .
.
解析试题分析:(1)由f(x)+f(1-x)= =1,能得到f(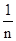 )+f(
)+f( 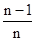 )=1.由此规律求值即可
)=1.由此规律求值即可
(2)由an=f(0)+f(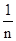 )+f(
)+f(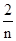 )+…+f(
)+…+f(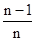 )+f(1)(n∈N*),知an=f(1)+f(
)+f(1)(n∈N*),知an=f(1)+f(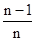 )+f(
)+f(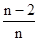 )+…+f(
)+…+f(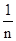 )+f(0)(n∈N*),由倒序相加法能得到an
)+f(0)(n∈N*),由倒序相加法能得到an
(3)由bn=2n+1•an,知bn=(n+1)•2n,由Sn=2•21+3•22+4•23+…+(n+1)•2n,利用错位相减法能求出Sn=n•2n+1,要使得不等式knSn>4bn恒成立,即kn2-2n-2>0对于一切的n∈N*恒成立,由此能够证明当k>4时,不等式knSn>bn对于一切的n∈N*恒成立.
解:(1)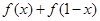 =
=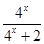 +
+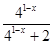 =
=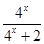 +
+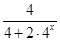 =1
=1
(2)∵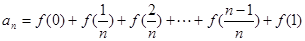 ①
①
∴ ②
②
由(Ⅰ),知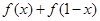 =1
=1
∴①+②,得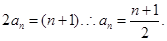
(3)∵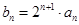 ,∴
,∴
∴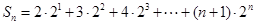 , ①
, ①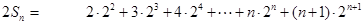 , ②
, ②
①-②得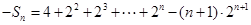
即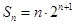 要使得不等式
要使得不等式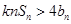 恒成立,即
恒成立,即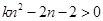 对于一切的
对于一切的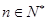 恒成立,
恒成立,
法一: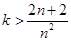 对一切的
对一切的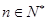 恒成立,
恒成立,
令 ,
,
∵ 在
在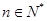 是单调递增的, ∴
是单调递增的, ∴ 的最小值为
的最小值为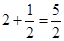
∴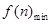 =
=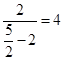 , ∴
, ∴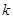
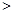
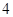 .
.
法二: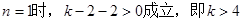 . 设
. 设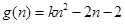
当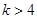 时,由于对称轴直线
时,由于对称轴直线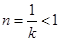 ,且
,且 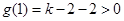 ,而函数
,而函数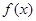 在
在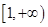 是增函数, ∴不等式
是增函数, ∴不等式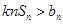 恒成立
恒成立
即当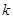
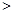
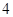 时,不等式
时,不等式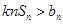 对于一切的
对于一切的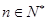 恒成立
恒成立
考点:本试题主要考查了数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.
点评:解题时要注意倒序相加法、错位相减法的灵活运用.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
14分)某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,且出版的书可全部销售完. 经出版社研究决定,新书投放市场后定价为 元/本(9≤
元/本(9≤ ≤11),预计一年的销售量为
≤11),预计一年的销售量为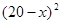 万本.
万本.
(1)求该出版社一年的利润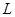 (万元)与每本书的定价
(万元)与每本书的定价 的函数关系式;
的函数关系式;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)
某市居民生活用水收费标准如下:
用水量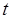 (吨) (吨) | 每吨收费标准(元) |
不超过 吨部分 吨部分 | 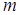 |
超过 吨不超过 吨不超过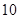 吨部分 吨部分 | 3 |
超过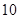 吨部分 吨部分 | 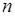 |
 吨,缴纳的水费为
吨,缴纳的水费为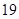 元;二月份用水量为
元;二月份用水量为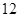 吨,缴纳的水费为
吨,缴纳的水费为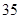 元.设某用户月用水量为
元.设某用户月用水量为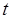 吨,交纳的水费为
吨,交纳的水费为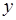 元.
元.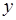 关于
关于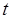 的函数关系式;
的函数关系式;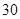 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com