练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知是x1方程logax+x-2016=0（a＞0，a≠1）的根，x2是方程ax+x-2016=0（a＞0，a≠1）的根，则x1+x2的值为（　　）
    A．2016B．2017C．1008D．1007

    分析 将x1，x2代入方程比较得到${a}^{{x}_{2}}$=x1，从而求出x1+x2=2016即可．

    解答 解：∵x1方程logax+x-2016=0（a＞0，a≠1）的根，
    x2是方程ax+x-2016=0（a＞0，a≠1）的根，
    ∴${a}^{{x}_{2}}$+x2=2016，①
    ${log}_{a}^{{a}^{{x}_{2}}}$+${a}^{{x}_{2}}$=2016，
    比较${log}_{a}^{{x}_{1}}$+x1=2016，
    得${a}^{{x}_{2}}$=x1，代此式代入①得
    x1+x2=2016，
    故选：A．

    点评 本题考查了根的存在性问题，考查至少、对数问题，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．若直线y=kx与曲线y=lnx有两个公共点，则实数k的取值范围为$（0，\frac{1}{e}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

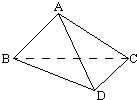    5．将一副三角板拼成直二面角A-BC-D，其中∠BAC=90°，AB=AC，∠BCD=90°，∠CBD=30°．
    （1）求证：平面BAD⊥平面CAD；
    （2）求BD与平面CAD所成的角的正切值；
    （3）若CD=2，求C到平面BAD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某工厂对某种产品的产量与成本的资料分析后有如表数据：
    产量x（千件）2356
    成本y（万元）78912
    经过分析，知道产量x和成本y之间具有线性相关关系．
    （1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程$\hat y$=$\hat b$x+$\hat a$；
    （2）试根据（1）求出的线性回归方程，预测产量为10千件时的成本．
    参考公式：回归直线的斜率和截距的最小二乘估计公式分别为$\hat b$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a$=$\overline y$-$\hat b$$\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=$\frac{ax-1}{{{x^2}+2}}$（x∈R），当x=2时f（x）取得极值．
    （1）求a的值；
    （2）求f（x）的单调区间；
    （3）若关于x的方程f（x）-2m+1=0在x∈[-2，1]时有解，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．方程2x•x2=1的实数解的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．a＜0，b＜0的一个必要条件为（　　）
    A．a+b＜0B．a-b＞0C．$\frac{a}{b}$＞1D．$\frac{a}{b}$＜-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1，则此双曲线的离心率e为（　　）
    A．$\frac{1}{2}$B．2C．2$\sqrt{2}$D．$\frac{\sqrt{7}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．对于两个图形F1，F2，我们将图形F1上的任意一点与图形F2上的任意一点间的距离中的最小值，叫作图形F1与图形F2的距离．若两个函数图象的距离小于1，称这两个函数互为“可及函数”．给出下列几对函数，其中互为“可及函数”的是（　　）
    A．f（x）=cosx，g（x）=2B．$f（x）={log_2}（{{x^2}-2x+5}），g（x）=sin\frac{π}{2}x$
    C．$f（x）=\sqrt{4-{x^2}}，g（x）=\frac{3}{4}x+\frac{15}{4}$D．$f（x）=x+\frac{2}{x}，g（x）=lnx+2$

    查看答案和解析>>

    同步练习册答案