
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
分析 (1)求线性回归直线方程要先求出均值,再由公式求出a,b的值,写出回归直线方程;
(2)令x=10,求出y即可.
解答 解:(1)由表中的数据得:$\overline x=\frac{2+3+5+6}{4}=4,\overline y=\frac{7+8+9+12}{4}=9$,$\sum_{i=1}^4{{x_i}{y_i}=2×7+3×8+5×9+6×12=155},\sum_{i=1}^4{x_i^2={2^2}+{3^2}+{5^2}+{6^2}=74}$,$\hat b=\frac{{\sum_{i=1}^4{{x_i}{y_i}-4\overline x\overline y}}}{{\sum_{i=1}^4{x_i^2-4{{\overline x}^2}}}}=\frac{155-4×4×9}{{74-4×{4^2}}}=\frac{11}{10}=1.1,\hat a=\overline y-\hat b\overline x=9-1.1×4=4.6$,
所以所求线性回归方程为$\hat y=1.1x+4.6$.
(2)由(1)得,当x=10时,$\hat y=1.1×10+4.6=15.6$,
即产量为10千件时,成本约为15.6万元.
点评 本题考查线性回归方程,解题的关键是理解并掌握求回归直线方程中参数a,b的值的方法,及求解的步骤.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 1008 | D. | 1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
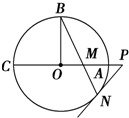 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com