
分析 (I)当n=1时,求得${a_1}=\frac{1}{2}$,n≥2时,an=Sn-Sn-1=an-1-an,$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}(n≥2)$,可知数列{an}是以$\frac{1}{2}$为首项,$\frac{1}{2}$为公比的等比数列,求得{an}的通项公式;
(II)由(I)可知,bn=nan=$\frac{n}{{2}^{n}}$,采用乘以公比“错位相减法”,即可求得{bn}的前n项和Sn.
解答 解:(I)当n=1时,S1=1-a1,
解得:${a_1}=\frac{1}{2}$.…(1分)
当n≥2时,an=Sn-Sn-1=(1-an)-(1-an-1)=an-1-an
化简整理得:$\frac{a_n}{{{a_{n-1}}}}=\frac{1}{2}(n≥2)$…(4分)
因此,数列{an}是以$\frac{1}{2}$为首项,$\frac{1}{2}$为公比的等比数列.
从而,${a_n}={(\frac{1}{2})^n}$.…(6分)
(II)由(I)可得,bn=nan=$\frac{n}{{2}^{n}}$,
∴${S_n}=1•\frac{1}{2}+2•{({\frac{1}{2}})^2}+3•{({\frac{1}{2}})^3}+4•{({\frac{1}{2}})^4}+…+n•{({\frac{1}{2}})^n}$,
$\frac{1}{2}{S_n}={({\frac{1}{2}})^2}+2•{({\frac{1}{2}})^3}+3•{({\frac{1}{2}})^4}+…+n•{({\frac{1}{2}})^{n+1}}$…(8分)
∴$\frac{1}{2}$Sn=$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+($\frac{1}{2}$)4+…+($\frac{1}{2}$)n-n•($\frac{1}{2}$)n+1,
$\frac{1}{2}$Sn=$\frac{\frac{1}{2}-(\frac{1}{2})^{n+1}}{1-\frac{1}{2}}$-n•($\frac{1}{2}$)n+1,
∴Sn=2-($\frac{1}{2}$)n-1-n•($\frac{1}{2}$)n.…(12分)
点评 本题考查等比数列通项公式,“错位相减法”求数列的前n项和,考查计算能力,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
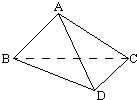 将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.
将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com