
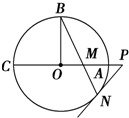
 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交分析 (Ⅰ)连结ON,运用切线的性质和切割线定理,结合等腰三角形的性质,即可得证;
(Ⅱ)延长BO交⊙于点D,连结DN,证得△BOM~△BND,可得对应边成比例,结合勾股定理,计算即可得到所求值.
解答 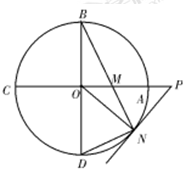 (Ⅰ)证明:连结ON,则ON⊥PN,且△OBN为等腰三角形,
(Ⅰ)证明:连结ON,则ON⊥PN,且△OBN为等腰三角形,
则∠OBN=∠ONB,
∵∠PMN=∠OMB=90°-∠OBN,∠PNM=90°-∠ONB,
∴∠PMN=∠PNM,
∴PM=PN.
由条件,根据切割线定理,有PN2=PA•PC,
所以PM2=PA•PC. 所以$\frac{PM}{PA}$=$\frac{PC}{PN}$;
(Ⅱ)解:OA=$\sqrt{3}$OM=$\sqrt{3}$,
∴OM=1,在Rt△BOM中,BM=$\sqrt{O{B}^{2}+O{M}^{2}}$=2.
延长BO交⊙于点D,连结DN,
可得∠BND=∠BOM,∠OBM=∠NBD,
则△BOM~△BND,
于是$\frac{BO}{BN}=\frac{BM}{BD}$,则$\frac{\sqrt{3}}{BN}$=$\frac{2}{2\sqrt{3}}$,
∴BN=3,
∴MN=BN-BM=1.
点评 本题考查三角形相似的判定和性质的运用,考查圆的切割线定理和直角三角形的勾股定理的运用,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
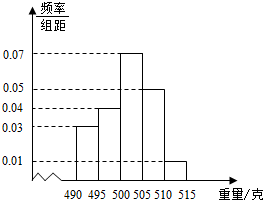 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
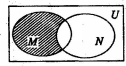 设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )
设集合$M=\{y|y={x^{\frac{1}{2}}},1≤x≤9\}$,N={x|y=log2(2-x)},则图中阴影部分表示的集合为( )| A. | {x|2≤x≤3} | B. | {x|1≤x≤2} | C. | $\{x|1≤x≤\sqrt{3}\}$ | D. | ∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com