
分析 若f(x)和g(x)存在隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k.利用函数的导数求出切线方程即可得到结论.
解答 解:令m(x)=f(x)-g(x)=x2-2elnx(x>0),再令m′(x)=2x-$\frac{2e}{x}$=0,解得 x=$\sqrt{e}$.
从而函数f(x)和g(x)的图象在x=$\sqrt{e}$处有公共点.此时公共点为($\sqrt{e}$,e),
因此存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,设隔离直线的斜率为k,则
隔离直线方程为y-e=k(x-$\sqrt{e}$),即y=kx-k $\sqrt{e}$+e.
由f(x)≥kx-k $\sqrt{e}$+e可得 x2-kx+k $\sqrt{e}$-e≥0当x∈R恒成立,
则△=k2-4k$\sqrt{e}$+4e=${(k-2\sqrt{e})}^{2}$≤0,只有k=2 $\sqrt{e}$时,等号成立,此时直线方程为:y=2 $\sqrt{e}$x-e.
同理证明,由g(x )≤kx-k $\sqrt{e}$+e,可得只有k=2 $\sqrt{e}$时,等号成立,此时直线方程为:y=2 $\sqrt{e}$x-e.
综上可得,函数f(x)和g(x)存在唯一的隔离直线y=2 $\sqrt{e}$x-e.
故答案为:y=2 $\sqrt{e}$x-e
点评 本题主要考查函数的切线和导数之间的关系,根据隔离直线的定义,确定隔离直线是两个函数的公共切线是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
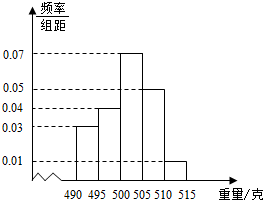 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克).重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com