
分析 (I)求导对m分类讨论即可得出单调性.
(II)由已知,关于x的方程$m=\frac{{1-{e^x}}}{x}+lnx$有正根.令$ϕ(x)=\frac{{1-{e^x}}}{x}+lnx,\;x>0$,利用研究其单调性极值与最值即可得出.
(III)令F(x)=xex-ex+1,可得F′(x)=xex>0.利用其单调性可得:$x>ln\frac{{{e^x}-1}}{x}=g(x)$.又由(I)知,m=-1时,f(x)=ex-x-1的最小值为f(0)=0,即ex-1>x.可得x∈(0,+∞)时,g(x)>0.综上,x∈(0,+∞)时,x>g(x)>0.由(I)知,当m≥-1时,f(x)在(0,+∞)上单调递增,可得f(g(x))<f(x)在x∈(0,+∞)上恒成立.当m<-1时,研究其单调性即可得出结论.
解答 解:(I)f'(x)=ex+m,
①当m≥0时,对?x∈R,有f'(x)>0.此时f(x)在(-∞,+∞)上单调递增.
②当m<0时,由f'(x)>0,得x>ln(-m);由f'(x)<0,得x<ln(-m).
此时函数f(x)的增区间为(ln(-m),+∞),减区间为(-∞,ln(-m)).
(II)由已知,关于x的方程$m=\frac{{1-{e^x}}}{x}+lnx$有正根.
令$ϕ(x)=\frac{{1-{e^x}}}{x}+lnx,\;x>0$,则$ϕ'(x)=\frac{{({1-x})({{e^x}-1})}}{x^2},\;x>0$.
由ϕ'(x)>0,得0<x<1;由ϕ'(x)<0,得x>1.
∴ϕ(x)在(0,1)上单调递增,在(1,+∞)上单调递减,ϕmax(x)=ϕ(1)=1-e.
∵关于x的方程$m=\frac{{1-{e^x}}}{x}+lnx$有正根.
∴m的最大值为1-e.
(III)令F(x)=xex-ex+1,则x>0时,F′(x)=xex>0.
∴F(x)在(0,+∞)上单调递增,x>0时,F(x)=xex-ex+1>F(0)=0.
故x∈(0,+∞)时,${e^x}>\frac{{{e^x}-1}}{x}$,即$x>ln\frac{{{e^x}-1}}{x}=g(x)$.
又由(I)知,m=-1时,f(x)=ex-x-1的最小值为f(0)=0,即ex-1>x.
∴x∈(0,+∞)时,g(x)=ln(ex-1)-lnx>0.
综上,x∈(0,+∞)时,x>g(x)>0.
由(I)知,当m≥-1时,f(x)在(0,+∞)上单调递增,
∴f(g(x))<f(x)在x∈(0,+∞)上恒成立.
当m<-1时,f(x)在(0,ln(-m))上单调递减,在(ln(-m),+∞)上单调递增.
当0<x<ln(-m)时,0<g(x)<x<ln(-m),∴f(g(x))>f(x),不满足题意.
故实数m的取值范围是[-1,+∞).
点评 本题考查了利用导数研究函数的单调性极值与最值、不等式的解法、方程的解法、等价转化方法,考查了分类讨论方法、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
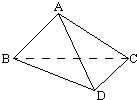 将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.
将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产量x(千件) | 2 | 3 | 5 | 6 |
| 成本y(万元) | 7 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com