
分析 (Ⅰ)利用点到直线的距离公式及离心率公式即可求得a和b的值,求得椭圆C的方程;
(Ⅱ)设直线l的方程,代入椭圆方程,利用韦达定理及$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OP}$,联立即可求得k的值,求得${k^2}=\frac{1}{14}<\frac{1}{2}$,椭圆C上是否存在点P,使得四边形OAPB为平行四边形.
解答 解:(Ⅰ)依题意$b=\frac{{\sqrt{2}}}{{\sqrt{1+1}}}=1$,${e^2}=\frac{c^2}{a^2}=\frac{{{a^2}-{b^2}}}{a^2}=\frac{1}{2}$,
∴a2=2,b2=1
∴椭圆C的方程为$\frac{x^2}{2}+{y^2}=1$…(5分)
(Ⅱ)由题意知直线的斜率存在,设直线的斜率为k,则其方程为y=k(x-2),
由$\left\{\begin{array}{l}y=k(x-2)\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,得(1+2k2)x2-8k2x+8k2-2=0…(6分)
∵△=64k4-4(8k2-2)(1+2k2)>0,
∴${k^2}<\frac{1}{2}$…(7分)
设A(x1,y1),B(x2,y2),假设在椭圆C上存在点P(x,y),使得四边形OAPB为平行四边形,
则有${x_1}+{x_2}=\frac{{8{k^2}}}{{1+2{k^2}}}$,${x_1}•{x_2}=\frac{{8{k^2}-2}}{{1+2{k^2}}}$,$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OP}$,
∴(x1,y1)+(x2,y2)=(x,y)
∴$x={x_1}+{x_2}=\frac{{8{k^2}}}{{1+2{k^2}}}$,$y={y_1}+{y_2}=k({x_1}-2)+k({x_2}-2)=-\frac{4k}{{1+2{k^2}}}$
∵点P(x,y)在椭圆C上,
∴${(\frac{{8{k^2}}}{{1+2{k^2}}})^2}+2{(-\frac{4k}{{1+2{k^2}}})^2}=2$即28k4+12k2-1=0
解得:${k^2}=\frac{1}{14}<\frac{1}{2}$,
所以在椭圆C上存在点P,使得四边形OAPB为平行四边形.…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:选择题
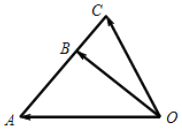
| A. | $\overrightarrow c=\frac{3}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow c=2\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow c=2\overrightarrow a-\overrightarrow b$ | D. | $\overrightarrow c=\frac{3}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
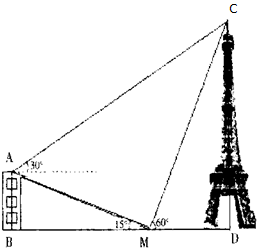 如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.
如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{2},\frac{1}{2}]$ | B. | [-2,2] | C. | (-∞,-2]∪[2,+∞) | D. | $(-∞,-\frac{1}{2}]∪[\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{128}$ | B. | $\frac{3}{256}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | m | 3.2 | 4.8 | 7.5 |
| A. | l | B. | 0.85 | C. | 0.7 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com