
分析 (Ⅰ)求得圆A的圆心和半径,运用直线平行的性质和等腰三角形的性质,可得EB=ED,再由圆的定义和椭圆的定义,可得E的轨迹为以A,B为焦点的椭圆,求得a,b,c,即可得到所求轨迹方程;
(Ⅱ)设直线l:x=my+1,代入椭圆方程,运用韦达定理和弦长公式,可得|MN|,由PQ⊥l,设PQ:y=-m(x-1),求得A到PQ的距离,再由圆的弦长公式可得|PQ|,再由四边形的面积公式,化简整理,运用不等式的性质,即可得到所求范围.
解答 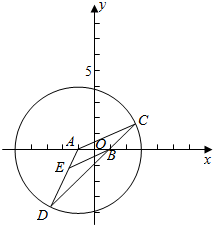 解:(Ⅰ)证明:圆x2+y2+2x-15=0即为(x+1)2+y2=16,
解:(Ⅰ)证明:圆x2+y2+2x-15=0即为(x+1)2+y2=16,
可得圆心A(-1,0),半径r=4,
由BE∥AC,可得∠C=∠EBD,
由AC=AD,可得∠D=∠C,
即为∠D=∠EBD,即有EB=ED,
则|EA|+|EB|=|EA|+|ED|=|AD|=4,
故E的轨迹为以A,B为焦点的椭圆,
且有2a=4,即a=2,c=1,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则点E的轨迹方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1(y≠0);
(Ⅱ)椭圆C1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,设直线l:x=my+1,
由PQ⊥l,设PQ:y=-m(x-1),
由$\left\{\begin{array}{l}{x=my+1}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$可得(3m2+4)y2+6my-9=0,
设M(x1,y1),N(x2,y2),
可得y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
则|MN|=$\sqrt{1+{m}^{2}}$•|y1-y2|=$\sqrt{1+{m}^{2}}$•$\sqrt{\frac{36{m}^{2}}{(3{m}^{2}+4)^{2}}+\frac{36}{3{m}^{2}+4}}$
=$\sqrt{1+{m}^{2}}$•$\frac{\sqrt{36(4{m}^{2}+4)}}{3{m}^{2}+4}$=12•$\frac{1+{m}^{2}}{3{m}^{2}+4}$,
A到PQ的距离为d=$\frac{|-m(-1-1)|}{\sqrt{1+{m}^{2}}}$=$\frac{|2m|}{\sqrt{1+{m}^{2}}}$,
|PQ|=2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{16-\frac{4{m}^{2}}{1+{m}^{2}}}$=$\frac{4\sqrt{3{m}^{2}+4}}{\sqrt{1+{m}^{2}}}$,
则四边形MPNQ面积为S=$\frac{1}{2}$|PQ|•|MN|=$\frac{1}{2}$•$\frac{4\sqrt{3{m}^{2}+4}}{\sqrt{1+{m}^{2}}}$•12•$\frac{1+{m}^{2}}{3{m}^{2}+4}$
=24•$\frac{\sqrt{1+{m}^{2}}}{\sqrt{3{m}^{2}+4}}$=24$\sqrt{\frac{1}{3+\frac{1}{1+{m}^{2}}}}$,
当m=0时,S取得最小值12,又$\frac{1}{1+{m}^{2}}$>0,可得S<24•$\frac{\sqrt{3}}{3}$=8$\sqrt{3}$,
即有四边形MPNQ面积的取值范围是[12,8$\sqrt{3}$).
点评 本题考查轨迹方程的求法,注意运用椭圆和圆的定义,考查直线和椭圆方程联立,运用韦达定理和弦长公式,以及直线和圆相交的弦长公式,考查不等式的性质,属于中档题.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=lgx | C. | y=2x | D. | y=$\frac{1}{\sqrt{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
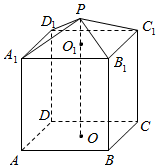 现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 9 | C. | 7 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4n}{m}$ | B. | $\frac{2n}{m}$ | C. | $\frac{4m}{n}$ | D. | $\frac{2m}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sin(2x+$\frac{π}{4}$) | B. | y=2sin(2x+$\frac{π}{3}$) | C. | y=2sin(2x-$\frac{π}{4}$) | D. | y=2sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com