
分析 根据已知中数列1$\frac{1}{2}$,2$\frac{1}{3}$,3$\frac{1}{4}$,4$\frac{1}{5}$,…的前四项,归纳可得数列的通项公式.
解答 解:数列1$\frac{1}{2}$,2$\frac{1}{3}$,3$\frac{1}{4}$,4$\frac{1}{5}$,…的值有两部分组成,
整数部分为1,2,3,4,…,
分数部分为:$\frac{1}{2}$,$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$,…
故整数部分为通项公式为n,分数部分的通项公式为$\frac{1}{n+1}$,
故数列1$\frac{1}{2}$,2$\frac{1}{3}$,3$\frac{1}{4}$,4$\frac{1}{5}$,…的一个通项公式为:n+$\frac{1}{n+1}$=$\frac{{n}^{2}+n+1}{n+1}$,
故答案为:$\frac{{n}^{2}+n+1}{n+1}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
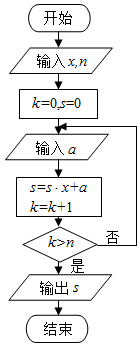 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com