
分析 (I)依题意知椭圆E的左顶点A(-2,0),由|AM|=|AN|,且MA⊥NA,可知△AMN为等腰直角三角形,设M(a-2,a),利用点M在E上,可得3(a-2)2+4a2=12,解得:a=$\frac{12}{7}$,从而可求△AMN的面积;
(II)设直线lAM的方程为:y=k(x+2),直线lAN的方程为:y=-$\frac{1}{k}$(x+2),联立$\left\{\begin{array}{l}y=k(x+2)\\ 3{x}^{2}+4{y}^{2}=12\end{array}\right.$消去y,得(3+4k2)x2+16k2x+16k2-12=0,利用韦达定理及弦长公式可分别求得|AM|=$\sqrt{1+{k}^{2}}$|xM-(-2)|=$\frac{12\sqrt{1+{k}^{2}}}{3+4{k}^{2}}$,|AN|=$\frac{12\sqrt{1+{(\frac{1}{k})}^{2}}}{3+4{(\frac{1}{k})}^{2}}$=$\frac{12k\sqrt{1+{k}^{2}}}{3{k}^{2}+4}$,
结合2|AM|=|AN|,可得$\frac{2}{3+4{k}^{2}}$=$\frac{k}{3{k}^{2}+4}$,整理后,构造函数f(k)=4k3-6k2+3k-8,利用导数法可判断其单调性,再结合零点存在定理即可证得结论成立.
解答 解:(I)由椭圆E的方程:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1知,其左顶点A(-2,0),
∵|AM|=|AN|,且MA⊥NA,∴△AMN为等腰直角三角形,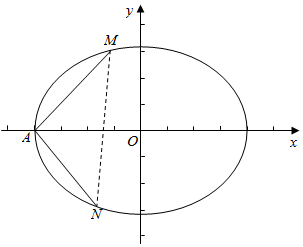
∴MN⊥x轴,设M的纵坐标为a,则M(a-2,a),
∵点M在E上,∴3(a-2)2+4a2=12,整理得:7a2-12a=0,∴a=$\frac{12}{7}$或a=0(舍),
∴S△AMN=$\frac{1}{2}$a×2a=a2=$\frac{144}{49}$;
(II)设直线lAM的方程为:y=k(x+2),直线lAN的方程为:y=-$\frac{1}{k}$(x+2),由$\left\{\begin{array}{l}y=k(x+2)\\ 3{x}^{2}+4{y}^{2}=12\end{array}\right.$消去y得:(3+4k2)x2+16k2x+16k2-12=0,∴xM-2=-$\frac{16{k}^{2}}{3+4{k}^{2}}$,∴xM=2-$\frac{16{k}^{2}}{3+4{k}^{2}}$=$\frac{6-8{k}^{2}}{3+4{k}^{2}}$,
∴|AM|=$\sqrt{1+{k}^{2}}$|xM-(-2)|=$\sqrt{1+{k}^{2}}$•$\frac{6-8{k}^{2}+6+8{k}^{2}}{3+4{k}^{2}}$=$\frac{12\sqrt{1+{k}^{2}}}{3+4{k}^{2}}$
∵k>0,
∴|AN|=$\frac{12\sqrt{1+{(\frac{1}{k})}^{2}}}{3+4{(\frac{1}{k})}^{2}}$=$\frac{12k\sqrt{1+{k}^{2}}}{3{k}^{2}+4}$,
又∵2|AM|=|AN|,∴$\frac{2}{3+4{k}^{2}}$=$\frac{k}{3{k}^{2}+4}$,
整理得:4k3-6k2+3k-8=0,
设f(k)=4k3-6k2+3k-8,
则f′(k)=12k2-12k+3=3(2k-1)2≥0,
∴f(k)=4k3-6k2+3k-8为(0,+∞)的增函数,
又f($\sqrt{3}$)=4×3$\sqrt{3}$-6×3+3$\sqrt{3}$-8=15$\sqrt{3}$-26=$\sqrt{675}$-$\sqrt{676}$<0,f(2)=4×8-6×4+3×2-8=6>0,
∴$\sqrt{3}$<k<2.
点评 本题考查直线与圆锥曲线的综合问题,常用的方法就是联立方程求出交点的横坐标或者纵坐标的关系,通过这两个关系的变形去求解,考查构造函数思想与导数法判断函数单调性,再结合零点存在定理确定参数范围,是难题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | ②④③① | B. | ④②③① | C. | ③①②④ | D. | ④①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com