
分析 (I)分当x<$-\frac{1}{2}$时,当$-\frac{1}{2}$≤x≤$\frac{1}{2}$时,当x>$\frac{1}{2}$时三种情况,分别求解不等式,综合可得答案;
(Ⅱ)当a,b∈M时,(a2-1)(b2-1)>0,即a2b2+1>a2+b2,配方后,可证得结论.
解答 解:(I)当x<$-\frac{1}{2}$时,不等式f(x)<2可化为:$\frac{1}{2}$-x-x-$\frac{1}{2}$<2,
解得:x>-1,
∴-1<x<$-\frac{1}{2}$,
当$-\frac{1}{2}$≤x≤$\frac{1}{2}$时,不等式f(x)<2可化为:$\frac{1}{2}$-x+x+$\frac{1}{2}$=1<2,
此时不等式恒成立,
∴$-\frac{1}{2}$≤x≤$\frac{1}{2}$,
当x>$\frac{1}{2}$时,不等式f(x)<2可化为:-$\frac{1}{2}$+x+x+$\frac{1}{2}$<2,
解得:x<1,
∴$\frac{1}{2}$<x<1,
综上可得:M=(-1,1);
证明:(Ⅱ)当a,b∈M时,
(a2-1)(b2-1)>0,
即a2b2+1>a2+b2,
即a2b2+1+2ab>a2+b2+2ab,
即(ab+1)2>(a+b)2,
即|a+b|<|1+ab|.
点评 本题考查的知识点是绝对值不等式的解法,不等式的证明,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
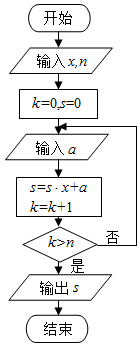 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com