
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 画出图形,设出抛物线方程,利用勾股定理以及圆的半径列出方程求解即可.
解答 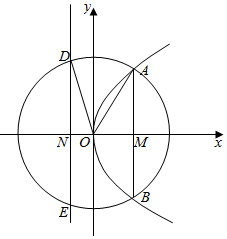 解:设抛物线为y2=2px,如图:|AB|=4$\sqrt{2}$,|AM|=2$\sqrt{2}$,
解:设抛物线为y2=2px,如图:|AB|=4$\sqrt{2}$,|AM|=2$\sqrt{2}$,
|DE|=2$\sqrt{5}$,|DN|=$\sqrt{5}$,|ON|=$\frac{p}{2}$,
xA=$\frac{(2\sqrt{2})^{2}}{2p}$=$\frac{4}{p}$,
|OD|=|OA|,
$\frac{16}{{p}^{2}}+8$=$\frac{{p}^{2}}{4}$+5,
解得:p=4.
C的焦点到准线的距离为:4.
故选:B.
点评 本题考查抛物线的简单性质的应用,抛物线与圆的方程的应用,考查计算能力.转化思想的应用.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ②④③① | B. | ④②③① | C. | ③①②④ | D. | ④①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.
如图,在平面直角坐标系xOy中,F是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,直线y=$\frac{b}{2}$与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
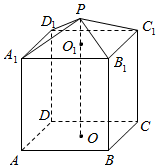 现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
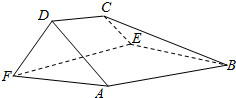 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com