
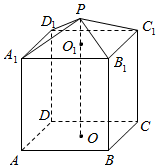
 现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.分析 (1)由正四棱柱的高O1O是正四棱锥的高PO1的4倍,可得PO1=2m时,O1O=8m,进而可得仓库的容积;
(2)设PO1=xm,则O1O=4xm,A1O1=$\sqrt{36-{x}^{2}}$m,A1B1=$\sqrt{2}$•$\sqrt{36-{x}^{2}}$m,代入体积公式,求出容积的表达式,利用导数法,可得最大值.
解答 解:(1)∵PO1=2m,正四棱柱的高O1O是正四棱锥的高PO1的4倍.
∴O1O=8m,
∴仓库的容积V=$\frac{1}{3}$×62×2+62×8=312m3,
(2)若正四棱锥的侧棱长为6m,
设PO1=xm,
则O1O=4xm,A1O1=$\sqrt{36-{x}^{2}}$m,A1B1=$\sqrt{2}$•$\sqrt{36-{x}^{2}}$m,
则仓库的容积V=$\frac{1}{3}$×($\sqrt{2}$•$\sqrt{36-{x}^{2}}$)2•x+($\sqrt{2}$•$\sqrt{36-{x}^{2}}$)2•4x=$-\frac{26}{3}$x3+312x,(0<x<6),
∴V′=-26x2+312,(0<x<6),
当0<x<2$\sqrt{3}$时,V′>0,V(x)单调递增;
当2$\sqrt{3}$<x<6时,V′<0,V(x)单调递减;
故当x=2$\sqrt{3}$时,V(x)取最大值;
即当PO1=2$\sqrt{3}$m时,仓库的容积最大.
点评 本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com