
| A. | ac<bc | B. | abc<bac | C. | alogbc<blogac | D. | logac<logbc |
分析 根据已知中a>b>1,0<c<1,结合对数函数和幂函数的单调性,分析各个结论的真假,可得答案.
解答 解:∵a>b>1,0<c<1,
∴函数f(x)=xc在(0,+∞)上为增函数,故ac>bc,故A错误;
函数f(x)=xc-1在(0,+∞)上为减函数,故ac-1<bc-1,故bac<abc,即abc>bac;故B错误;
logac<0,且logbc<0,logab<1,即$\frac{{log}_{c}b}{{log}_{c}a}$=$\frac{{log}_{a}c}{{log}_{b}c}$<1,即logac>logbc.故D错误;
0<-logac<-logbc,故-blogac<-alogbc,即blogac>alogbc,即alogbc<blogac,故C正确;
故选:C
点评 本题考查的知识点是不等式的比较大小,熟练掌握对数函数和幂函数的单调性,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{36}{65}$ | B. | -$\frac{3}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{48}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=lgx | C. | y=2x | D. | y=$\frac{1}{\sqrt{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
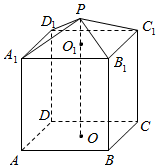 现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com