
| A. | 0 | B. | 3 | C. | 4 | D. | 5 |
分析 作出不等式组对应的平面区域,目标函数的几何意义是直线的纵截距,利用数形结合即可求z的取值范围.
解答 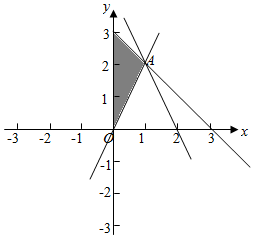 解:作出不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x+y≤3}\\{x≥0}\end{array}\right.$对应的平面区域如图:(阴影部分).
解:作出不等式组$\left\{\begin{array}{l}{2x-y≤0}\\{x+y≤3}\\{x≥0}\end{array}\right.$对应的平面区域如图:(阴影部分).
设z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点A时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{2x-y=0}\\{x+y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,即A(1,2),
代入目标函数z=2x+y得z=1×2+2=4.
即目标函数z=2x+y的最大值为4.
故选:C.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.


科目:高中数学 来源: 题型:选择题
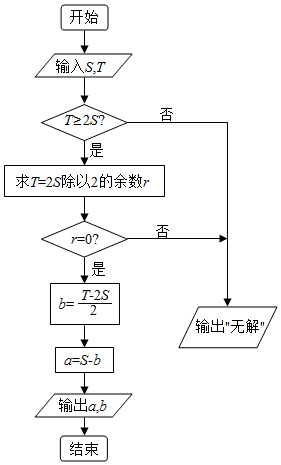 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )| A. | S=40,T=120 | B. | S=40,T=126 | C. | S=42,T=126 | D. | S=42,T=130 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=lgx | C. | y=2x | D. | y=$\frac{1}{\sqrt{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{8}{25}$ | D. | $\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ②④③① | B. | ④②③① | C. | ③①②④ | D. | ④①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com