
分析 由于y=log2(2-x)在[0,k)上是递减函数,再由函数f(x)的值域是[-1,1],得到k的范围,再由y=x3-3x2+3的图象,结合函数的值域[-1,1],从而得到a的取值范围.
解答  解:由于y=log2(2-x)在[0,k)上是递减函数,
解:由于y=log2(2-x)在[0,k)上是递减函数,
且x=0时,y=1,x=$\frac{3}{2}$时,y=-1,故0<k≤$\frac{3}{2}$,
画出函数f(x)的图象,令x3-3x2+3=1,
解得x=1,1+$\sqrt{3}$,1-$\sqrt{3}$(舍去),
令g(x)=x3-3x2+3,则g′(x)=3x2-6x,
由g′(x)=0,得x=0或x=2.
∴当x=2时,函数g(x)有极小值-1.
由于存在k使得函数f(x)的值域是[-1,1],
故a的取值范围是[2,1+$\sqrt{3}$].
故答案为:[2,1+$\sqrt{3}$].
点评 本题考查分段函数的图象和应用,考查函数的单调性和值域,考查数形结合的能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | 增函数 | B. | 减函数 | ||
| C. | 既不是增函数也不是减函数 | D. | 无法判断 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
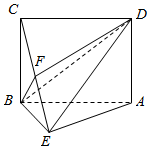 已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=2$\sqrt{3}$,EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=2$\sqrt{3}$,EB=BC=2,点F为CE上一点,且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 x,y满足条件$\left\{{\begin{array}{l}{3x-5y+6≥0}\\{2x+3y-15≤0}\\{y≥0}\end{array}}\right.$,则z=x-2y的最小值是-3.
x,y满足条件$\left\{{\begin{array}{l}{3x-5y+6≥0}\\{2x+3y-15≤0}\\{y≥0}\end{array}}\right.$,则z=x-2y的最小值是-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
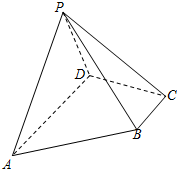 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=∠BCD=90°,BC=2,$CD=\sqrt{3}$,PD=4,∠PDA=60°,且平面PAD⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,∠ADC=∠BCD=90°,BC=2,$CD=\sqrt{3}$,PD=4,∠PDA=60°,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com