
分析 由递推公式依次求出数列的前4项,由归纳推理得出数列的通项公式.
解答 解:由${a_1}=\frac{1}{4}$,${a_n}=\frac{1}{2}{a_{n-1}}+{2^{-n}}$(n≥2),
得${a_1}=\frac{1}{4}$,
${a}_{2}=\frac{1}{2}{a}_{1}+{2}^{-2}=\frac{3}{8}$,
${a}_{3}=\frac{1}{2}{a}_{2}+{2}^{-3}=\frac{5}{16}$,
${a}_{4}=\frac{1}{2}{a}_{3}+{2}^{-4}=\frac{7}{32}$
…
归纳得$a{\;}_n=\frac{2n-1}{{{2^{n+1}}}}$.
点评 本题考查数列的通项公式,考查学生的计算能力,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,x2-1<2lnx | B. | ?x>0,x2-1<2lnx | C. | ?x>0,x2-1<2lnx | D. | ?x≤0,x2-1<2lnx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | “?x∈R,x3-x2+1≤0”的否定是“?x∈R,x3-x2+1>0“ | |
| D. | “△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
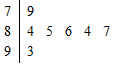 如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 84,84 | B. | 84,85 | C. | 85,84 | D. | 85,85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,$\frac{π}{2}$) | B. | (3,-$\frac{π}{2}$) | C. | (3,0) | D. | (3,π) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com