
分析 (1)依题意,可求得椭圆的半长轴a=6,半焦距c=2,从而可求得半短轴b,于是可得椭圆的方程;
(2)先确定a的值,再分类讨论,求出b的值,即可得到双曲线的标准方程.
解答 解:(1)由于椭圆的焦点在x轴上,长轴长为10,
则2a=10,a=5,
又由椭圆的离心率为$\frac{4}{5}$,
则$\frac{c}{a}=\frac{c}{5}=\frac{4}{5}$,
故c=4.
∴b2=a2-c2=9.
故所求椭圆的标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$;
(2)由题意2a=6,∴a=3.
当焦点在x轴上时,∵双曲线的渐近线方程为y=±$\frac{3}{2}$x,
∴$\frac{b}{3}=\frac{3}{2}$,∴b=$\frac{9}{2}$,
∴方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{\frac{81}{4}}=1$;
当焦点在y轴上时,∵双曲线的渐近线方程为y=±$\frac{3}{2}$x,
∴$\frac{3}{b}=\frac{3}{2}$,∴b=2,
∴方程为$\frac{{y}^{2}}{9}-\frac{{x}^{2}}{4}=1$.
故双曲线的标准方程为:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{\frac{81}{4}}=1$或$\frac{{y}^{2}}{9}-\frac{{x}^{2}}{4}=1$.
点评 本题考查椭圆的标准方程和双曲线的标准方程,考查理解与运算能力以及分类讨论的数学思想,属于基础题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
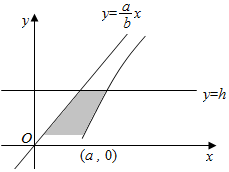 我们在学习立体几何推导球的体积公式时,用到了祖日恒原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),与x轴,直线y=h(h>0)及渐近线$y=\frac{b}{a}x$所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖日恒原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0),与x轴,直线y=h(h>0)及渐近线$y=\frac{b}{a}x$所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com