
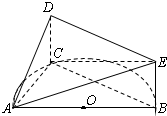
 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,tan∠EAB=| 1 |
| 4 |
| 2 |
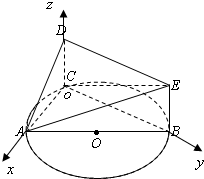 (Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),
(Ⅰ)证明:∵AB是直径,∴BC⊥AC…(1分),| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 12 |
| 4 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
| AB |
| 2 |
| 2 |
| BE |
| DE |
| 2 |
| DA |
| 2 |
| n |
|
|
| n |
| 2 |
| n2 |
|
|
| n |
| n |
| n |
| ||||
|
|
| 1 | ||||
|
| ||
| 6 |
| n |
| n |
| ||
| 6 |


科目:高中数学 来源: 题型:
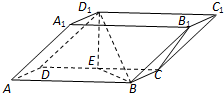 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明
小昆和小鹏两人站成一列,背着墙,面朝太阳,小昆靠近墙,在太阳光照射下,小昆的头部影子正好落在墙角处.如果小昆身高为1.6m,离墙距离为3m,小鹏的身高1.5m,离墙的距离为5m,则小鹏的身影是否在小昆的脚下,请通过计算说明查看答案和解析>>
科目:高中数学 来源: 题型:
| kx |
| |x|+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=
如图,在直三棱柱ABC-A′B′C′中,AB=AA′=AC=2,∠BAC=| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com