练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
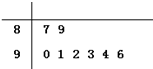
    10．某校高二年级8个班参加合唱比赛的得分如面茎叶图所示，则这组数据的中位数和平均数为91.5和91.5．

    分析 根据茎叶图写出这组数据，把数据按照从大到小排列，最中间的一个或最中间两个数字的平均数就是中位数，平均数只要代入平均数的公式得到结果．

    解答 解：由茎叶图可知：这组数据为87，89，90，91，92，93，94，96，
    所以其中位数为$\frac{91+92}{2}$=91.5，
    平均数为$\frac{1}{8}$（87+89+90+91+92+93+94+96）=91.5，
    故答案为：91，5； 91.5

    点评 本题考查茎叶图的基础知识，考查同学们的识图能力，考查中位数与平均数的求法．在求中位数时，首先要把这列数字按照从小到大或从的大到小排列，找出中间一个数字或中间两个数字的平均数即为所求

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．如图，网格纸上正方形小格的边长为1，图中粗线画出的是某零件的三视图，则该零件的表面积为（　　）
    A．37πB．46πC．50πD．54π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．以曲线C：y=x2（x≥0）上某一点A为切点作一切线l，使之与曲线C以及x轴所围成的图形的面积为$\frac{2}{3}$，求切线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率依次成等差数列，第2小组的频数为15，则抽取的学生人数为60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知在△ABC中，若sinA+cosA=$\frac{1}{5}$，求sinAcosA+sinA-cosA的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知复数$z=\frac{3-2i}{{{i^{2015}}}}$（i是虚数单位），则复数z所对应的点的坐标为（2，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如下频率分布直方图：
    （Ⅰ） 估计这500件产品质量指标值的样本平均数$\overline x$．
    （Ⅱ）由频率分布直方图可以认为，这种总产品的质量指标值Z近似服从正态分布N（μ，δ2），其中μ近似为样本平均数$\overline x$，δ2近似为样本方差s2．（由样本估计得样本方差为s2=150）
    （i）利用该正态分布，求P（Z＜212.2）；
    （ii）若将这种产品质量指标值位于这三个区间（-∞，187.8）（187.8，212.2）（212.2．，+∞）的等级分别为二等品，一等品，优质品，这三类等级的产品在市场上每件产品的利润分别为2元，5元，10元．某商户随机从该企业批发100件这种产品后卖出获利，记X表示这100件产品的利润，利用正态分布原理和（i）的结果，求EX．
    附：$\sqrt{150}$≈12.2．若Z～N（μ，δ2），则P（μ-δ＜Z＜μ+δ）=0.6826，P（μ-2δ＜Z＜μ+2δ）=0.9544．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．如图，过抛物线y2=2px（p＞0）焦点F的直线交抛物线于A，B两点，O为坐标原点，C为抛物线准线与x轴的交点，且∠CFA=135°，则tan∠ACB=2$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知集合M=|x|2x-3＜1|，集合N=|x|-1＜x＜3|，则M∩N=（　　）
    A．MB．NC．|x|-1＜x＜2|D．|x|x＜3|

    查看答案和解析>>

    同步练习册答案