
(1)求经过点A(﹣5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程.
(2)过点A(8,6)引三条直线l1,l2,l3,它们的倾斜角之比为1:2:4,若直线l2的方程是y=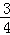 x,求直线l1,l3的方程.
x,求直线l1,l3的方程.
(1)x+2y+1=0或2x+5y=0.
(2)x﹣3y+10=0,24x﹣7y﹣150=0.
【解析】
试题分析:(1)当截距都为零时,设所求的直线方程为y=kx,待定系数法求出k,从而得到直线方程;当截距都不为零时,设所求直线方程为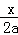 +
+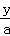 =1,待定系数法求a.
=1,待定系数法求a.
(2)直线l2的倾斜角为α,则tanα= ,求出
,求出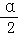 、2α 的正切值,即得到l1,,l3 的斜率,点斜式写l1,,l3 的
、2α 的正切值,即得到l1,,l3 的斜率,点斜式写l1,,l3 的
方程,并化为一般式.
【解析】
(1)①当横截距、纵截距都为零时,设所求的直线方程为y=kx,将(﹣5,2)代入y=kx中,得k=﹣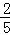 ,此时,直线方程为y=﹣
,此时,直线方程为y=﹣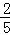 x,即2x+5y=0.
x,即2x+5y=0.
②当横截距、纵截距都不是零时,设所求直线方程为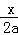 +
+ =1,
=1,
将(﹣5,2)代入所设方程,
解得a=﹣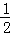 ,
,
此时,直线方程为x+2y+1=0.
综上所述,所求直线方程为
x+2y+1=0或2x+5y=0.
(2)设直线l2的倾斜角为α,则tanα= .
.
于是tan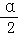 =
=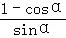 =
= =
=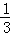 ,
,
tan2α=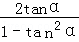 =
=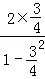 =
= ,
,
所以所求直线l1的方程为y﹣6=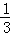 (x﹣8),
(x﹣8),
即x﹣3y+10=0,
l3的方程为y﹣6=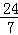 (x﹣8),
(x﹣8),
即24x﹣7y﹣150=0.


科目:高中数学 来源:[同步]2014年湘教版选修1-1 2.1 椭圆练习卷(解析版) 题型:选择题
(3分)已知椭圆以两条坐标轴为对称轴,一个顶点是(0,13),另一个顶点是(﹣10,0),则焦点坐标为( )
A.(±13,0) B.(0,±10) C.(0,±13) D.(0,±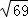 )
)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修二 3.1 弧度制与任意角练习卷1(解析版) 题型:填空题
(5分)α是第二象限角,P(x,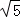 )为其终边上一点,且cosα=
)为其终边上一点,且cosα=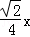 ,则sinα= .
,则sinα= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:填空题
(5分)若直线l经过点(a﹣2,﹣1)和(﹣a﹣2,1),且与经过点(﹣2,1),斜率为﹣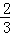 的直线垂直,则实数a的值为 .
的直线垂直,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修三 7.1 解析几何初步练习卷(解析版) 题型:选择题
(4分)与直线x+4y﹣4=0垂直,且与抛物线y=2x2相切的直线方程为( )
A.4x﹣y+1=0 B.4x﹣y﹣1=0 C.4x﹣y﹣2=0 D.4x﹣y+2=0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.3平均值不等式练习卷(解析版) 题型:选择题
求证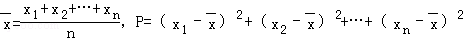 ,q=(x1﹣a)2+(x2﹣a)2+…+(xn﹣a)2若
,q=(x1﹣a)2+(x2﹣a)2+…+(xn﹣a)2若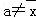 则一定有( )
则一定有( )
A.P>q B.P<q C.P、q的大小不定 D.以上都不对
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷(解析版) 题型:选择题
(2013•南开区一模)已知A={x||2x﹣1|<5},B={x|x2﹣5x+4<0},C=(1,3),则“x∈A∩B”是“x∈C”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com