
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(1)求椭圆的方程;
(2)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求证:直线
,求证:直线![]() 的斜率与直线MN的斜率之积为定值.
的斜率与直线MN的斜率之积为定值.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(﹣2![]() ,0),B
,0),B![]() ,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于
,M(x,y)是曲线C上的动点,且直线AM与BM的斜率之积等于![]() .
.
(1)求曲线C方程;
(2)过D(2,0)的直线l(l与x轴不垂直)与曲线C交于E,F两点,点F关于x轴的对称点为F′,直线EF′与x轴交于点P,求△PEF的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
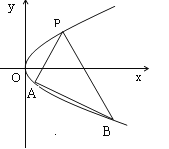
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于一个向量组![]() ,令
,令![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 是该向量组的“长向量”
是该向量组的“长向量”
(1)若![]() 是向量组
是向量组![]() 的“长向量”,且
的“长向量”,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,
,![]() ,
,![]() 均是向量组
均是向量组![]() 的“长向量”,试探究
的“长向量”,试探究![]() ,
,![]() ,
,![]() 的等量关系并加以证明.
的等量关系并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,并统计他们的日加工零件数,得到以下数据;

(1)已知日加工零件数在![]() 范围内的5名员工中,有3名男工,2名女工,现从中任取两名进行指导,求他们性别不同的概率;
范围内的5名员工中,有3名男工,2名女工,现从中任取两名进行指导,求他们性别不同的概率;
(2)完成频率分布直方图,并估计全体新员工每天加工零件数的平均数(每组数据以中点值代替);
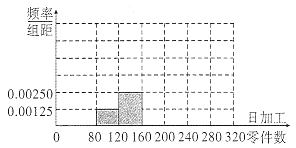
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com