
分析 (1)列方程组计算a,b得出f(x);
(2)计算x1,x2,x3,根据前三项猜想通项公式,并用数学归纳法证明.
解答 解:(1)∵f(1)=$\frac{1}{4}$,f(-2)=1,
∴$\left\{\begin{array}{l}{\frac{b+1}{(a+1)^{2}}=\frac{1}{4}}\\{\frac{-2b+1}{(-2a+1)^{2}}=1}\end{array}\right.$,又a>0,解得a=1,b=0.
∴f(x)=$\frac{1}{(x+1)^{2}}$.
(2)x1=1-f(1)=1-$\frac{1}{4}$=$\frac{3}{4}$;
x2=(1-f(1))(1-f(2))=$\frac{3}{4}×$$\frac{8}{9}$=$\frac{2}{3}$,
x3=(1-f(1))(1-f(2))(1-f(3))=$\frac{5}{8}$,
猜想:xn=$\frac{n+2}{2n+2}$.
证明:①当n=1时,猜想显然成立,
②假设n=k(k≥1)时猜想成立,即xk=$\frac{k+2}{2k+2}$.
则xk+1=xk(1-f(k+1))=$\frac{k+2}{2k+2}$•(1-$\frac{1}{(k+2)^{2}}$)=$\frac{k+2}{2k+2}•$$\frac{(k+1)(k+3)}{(k+2)^{2}}$=$\frac{k+3}{2(k+2)}$=$\frac{k+1+2}{2(k+1)+2}$.
∴当n=k+1时,猜想成立.
∴对任意n∈N+,都有xn=$\frac{n+2}{2n+2}$.
点评 本题考查了待定系数法求解析式,数学归纳法证明,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:解答题
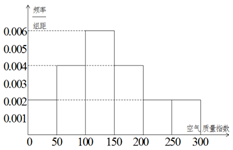 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度 污染 | 4级中度 污染 | 5级重度 污染 | 6级严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{3}$个单位长度 | D. | 向右平移$\frac{π}{3}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com