Question

5．设变量x，y满足约束条件$\left\{{\begin{array}{l}{y≥0}\\{x-y≥0}\\{2x-y-1≤0}\end{array}}$，且目标函数z=$\frac{x}{a}$+$\frac{y}{b}$（a，b为正数）的最大值为1，则a+b的最小值为（　　）

• A． $\sqrt{2}$
• B． 4
• C． 2
• D． $2\sqrt{2}$

Answer 1

分析 画出满足条件的平面区域，求出角点的坐标，结合图象得到$\frac{1}{a}$+$\frac{1}{b}$=1，根据基本不等式的性质求出a+b的最小值即可．

解答 解：画出满足条件的平面区域，如图示：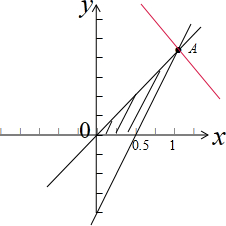
，
由$\left\{\begin{array}{l}{x-y=0}\\{2x-y-1=0}\end{array}\right.$，解得A（1，1），
由z=$\frac{x}{a}$+$\frac{y}{b}$（a，b为正数）得：y=-$\frac{b}{a}$x+bz，-$\frac{b}{a}$＜0
平移直线y=-$\frac{b}{a}$x，结合图象直线过A（1，1）时，
z最大，故$\frac{1}{a}$+$\frac{1}{b}$=1，
∴（a+b）（$\frac{1}{a}$+$\frac{1}{b}$）=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4，
当且仅当a=b=2时“=”成立，
故选：B．

点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道中档题．