
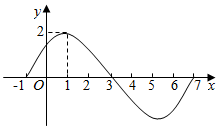
 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).分析 (1)根据最大值得出A,利用周期求出ω,特殊特殊点计算φ;
(2)利用函数的对称性得出g(x)=f(4-x).
解答 解:(1)由函数图象可知y=Asin(ωx+φ)的最大值为2,周期为8,
∴A=2,$\frac{2π}{ω}=8$,即ω=$\frac{π}{4}$.
由图象可知当x=1时,函数y=Asin(ωx+φ)取得最大值2,
∴2sin($\frac{π}{4}$+φ)=2,∴$\frac{π}{4}+$φ=$\frac{π}{2}$+2kπ,于是φ=$\frac{π}{4}$+2kπ.
∵φ∈(-$\frac{π}{2}$,$\frac{π}{2}$),∴φ=$\frac{π}{4}$.
∴y=2sin($\frac{π}{4}x+\frac{π}{4}$).
(2)∵函数y=g(x)与y=f(x)=Asin(ωx+φ)的图象关于直线x=2对称,
∴g(x)=f(4-x)=2sin[$\frac{π}{4}$(4-x)+$\frac{π}{4}$]=-2sin($\frac{π}{4}x$-$\frac{π}{4}$).
点评 本题考查了三角函数的图象与性质,函数图象的变换,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+1)2=2 | B. | (x+1)2+(y-1)2=2 | C. | (x-1)2+(y+1)2=4 | D. | (x+1)2+(y-1)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 若y=f(x)的图象如图所示,定义F(x)=$\int_0^x{f(t)dt$,x∈[0,1],则下列对F(x)的性质描述正确的有(1)(2)(4).(把所有正确的序号都填上)
若y=f(x)的图象如图所示,定义F(x)=$\int_0^x{f(t)dt$,x∈[0,1],则下列对F(x)的性质描述正确的有(1)(2)(4).(把所有正确的序号都填上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com