
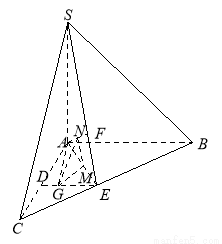
(本题满分12分)如图,在三棱锥 中,
中,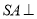 底面
底面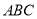 ,
,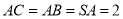 ,
, ,
, 分别是
分别是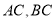 的中点,
的中点,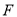 在
在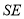 上,且
上,且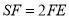 .
.

(1)求证: 平面
平面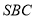 ;
;
(2)在线段上 上是否存在点
上是否存在点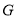 ,使二面角
,使二面角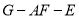 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)详见解析 (2)满足条件的点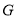 存在,且
存在,且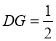
【解析】
试题分析:第(1)问证明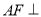 平面
平面 ,基本思路是证明
,基本思路是证明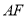 与平面
与平面 内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点
内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点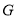 的预设位置,二是二面角
的预设位置,二是二面角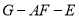 的位置.涉及空间二面角的问题,可以从两个不同的方法上得到求解,即常规法和向量法.
的位置.涉及空间二面角的问题,可以从两个不同的方法上得到求解,即常规法和向量法.
试题解析:(1)由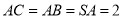 ,
,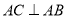 ,
,
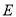 是
是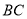 的中点,得
的中点,得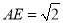 .
.
因为 底面
底面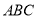 ,所以
,所以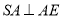 .
.
在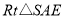 中,
中, ,所以
,所以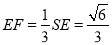 .
.
因此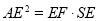 ,又因为
,又因为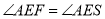 ,
,
所以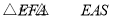 ,
,
则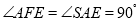 ,即
,即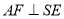 .
.
因为 底面
底面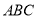 ,所以
,所以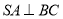 ,又
,又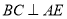 ,
,
所以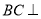 底面
底面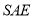 ,则
,则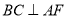 .
.
又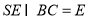 ,所以
,所以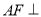 平面
平面 .
.
(2)解法1(常规法):假设满足条件的点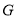 存在,并设
存在,并设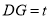 .
.
过点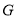 作
作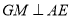 交
交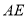 于点
于点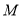 ,
,
又由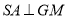 ,
,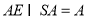 ,得
,得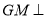 平面
平面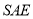 .
.
作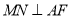 交
交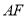 于点
于点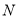 ,连结
,连结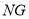 ,则
,则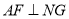 .
.
于是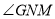 为二面角
为二面角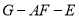 的平面角,
的平面角,
即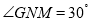 ,由此可得
,由此可得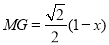 .
.
由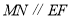 ,得
,得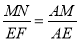 ,于是有
,于是有 ,
,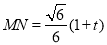 .
.
在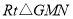 中,
中,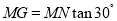 ,即
,即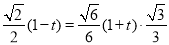 ,解得
,解得 .
.
于是满足条件的点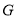 存在,且
存在,且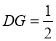 .
.
(2)解法2(向量法):假设满足条件的点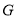 存在,并设
存在,并设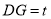 .以
.以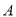 为坐标原点,分别以
为坐标原点,分别以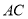 ,
,
 ,
,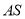 为
为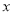 ,
,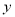 ,
, 轴建立空间直线坐标系
轴建立空间直线坐标系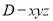 ,则
,则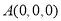 ,
,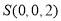 ,
,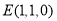 ,
,
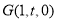 .
.
由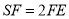 得
得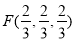 .
.
所以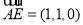 ,
,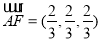 ,
, .
.
设平面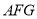 的法向量为
的法向量为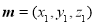 ,则
,则
 ,即
,即 ,取
,取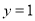 ,得
,得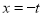 ,
,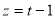 ,即
,即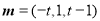 .
.
设平面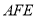 的法向量为
的法向量为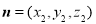 ,则
,则
 ,即
,即 ,取
,取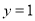 ,得
,得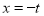 ,
,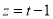 ,即
,即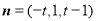 .
.
由二面角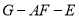 的大小为
的大小为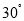 ,得
,得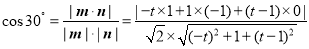 ,
,
化简得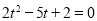 ,又
,又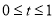 ,求得
,求得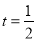 .
.
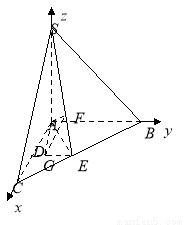
于是满足条件的点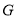 存在,且
存在,且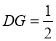 .
.
考点:线面关系的平行或垂直的证明及空间角的计算.


科目:高中数学 来源: 题型:
为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位: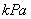 )的分组区间为
)的分组区间为 ,
, ,
, ,
, ,
, ,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为
(A)1(B)8(C)12(D)18
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州地区7校高三上学期期末模拟联考理科数学试卷(解析版) 题型:选择题
已知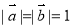 向量
向量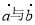 的夹角为120°,且
的夹角为120°,且 ,则实数t的值为( )
,则实数t的值为( )
 .-1 B.1 C.-2 D.2
.-1 B.1 C.-2 D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品文科数学试卷(解析版) 题型:选择题
已知双曲线 :
: 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于
的准线分别交于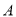 ,
, 两点,
两点,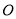 为坐标原点,若双曲线
为坐标原点,若双曲线 的离心率为2,
的离心率为2, 的面积为
的面积为 ,则
,则 的内切圆半径为( )
的内切圆半径为( )
A. B.
B. C.
C.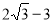 D.
D.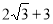
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品文科数学试卷(解析版) 题型:选择题
某中学从甲、乙两个艺术班中选出7名学生参加市级才艺比赛,他们取得的成绩(满分100)的茎叶图如图所示,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则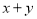 的值为( )
的值为( )

A.6 B.8 C.9 D.11
查看答案和解析>>
科目:高中数学 来源:2014-2015学年稳派新课程高三2月精品理科数学试卷(解析版) 题型:填空题
(1)若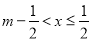 (其中
(其中 为正数),则称
为正数),则称 为离实数
为离实数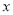 最近的正数,记作
最近的正数,记作 ,即
,即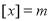
 ,则
,则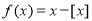 的值域是 ;
的值域是 ;
(2)设集合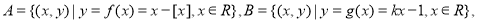 若集合
若集合 的子集恰有4个,则实数
的子集恰有4个,则实数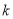 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:填空题
如图,在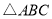 中,点
中,点 是
是 的中点,过点
的中点,过点 的直线分别交直线
的直线分别交直线 ,
, 于不同的两点
于不同的两点 ,若
,若 ,
,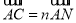 ,则
,则 的值为 .
的值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com