
【题目】已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() ,
,![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
【答案】(Ⅰ)曲线C1的普通方程是![]() ,曲线C2的普通方程是2x+3y﹣10=0.
,曲线C2的普通方程是2x+3y﹣10=0.
(Ⅱ)最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】
试题分析:(1)利用平方法将![]() 的参数方程消去参数可得到曲线
的参数方程消去参数可得到曲线![]() 普通方程,利用代入法将
普通方程,利用代入法将![]() 的参数方程消去参数可得到
的参数方程消去参数可得到![]() 的普通方程;(2)根据曲线
的普通方程;(2)根据曲线![]() 的参数方程设点
的参数方程设点![]() 为
为![]() 曲线上任意一点,利用点到直线距离公式求出点
曲线上任意一点,利用点到直线距离公式求出点![]() 到直线的距离
到直线的距离![]() ,利用三角函数的有界性可得曲线
,利用三角函数的有界性可得曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
试题解析:(1)曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),则
为参数),则![]() ,
,
∵![]() ,
,
可得![]() ,
,
∴曲线![]() 的普通方程是
的普通方程是![]() ;
;
曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),消去参数
为参数),消去参数,
![]() ,代入
,代入![]() ,即
,即![]()
∴曲线![]() 的普通方程是
的普通方程是![]() .
.
(2)设点![]() 为曲线
为曲线![]() 上任意一点,则点
上任意一点,则点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则
![]()
∵![]()
∴![]()
∴![]()


科目:高中数学 来源: 题型:
【题目】“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其主视图和侧视图完全相同时,它的俯视图可能是( ) 
A.
B.
C.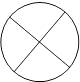
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() =
= ![]() =
=![]() =
= ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.

(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆![]() 的圆心在直线
的圆心在直线![]() 上,且过点
上,且过点![]() ,与直线
,与直线![]() 相切.
相切.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点.求实数
两点.求实数![]() 的取值范围.
的取值范围.
(![]() )在(
)在(![]() )的条件下,是否存在实数
)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() 必过
必过![]() ;
;
④在一个2×2列联表中,由计算得![]() =13.079,则有99%的把握确认这两个变量间有关系(其中
=13.079,则有99%的把握确认这两个变量间有关系(其中![]() );
);
其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中:
①存在一个平面与正方体的12条棱所成的角都相等;
②存在一个平面与正方体的6个面所成较小的二面角都相等;
③存在一条直线与正方体的12条棱所成的角都相等;
④存在一条直线与正方体的6个面所成的角都相等.
其中真命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com