
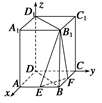
 ,侧棱长为4,E、F分别为棱AB、BC的中点.
,侧棱长为4,E、F分别为棱AB、BC的中点.
 ,2
,2 ,0),E(2
,0),E(2 ,
, ,0),
,0), ,2
,2 ,0),D1(0,0,4),
,0),D1(0,0,4), ,2
,2 ,4).
,4).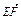 =(-
=(- ,
, ,0),
,0),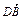 =(2
=(2 ,2
,2 ,0),
,0),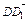 =(0,0,4),
=(0,0,4),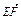 ·
·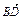 =0,
=0,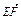 ·
·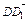 =0.
=0.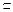 平面B1EF,∴平面B1EF⊥平面BDD1B1.
平面B1EF,∴平面B1EF⊥平面BDD1B1.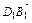 =(2
=(2 ,2
,2 ,0),
,0),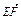 =(-
=(- ,
, ,0),
,0),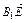 =(0,-
=(0,- ,-4).
,-4).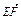 ,n⊥
,n⊥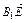
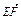 =(x,y,z)·(-
=(x,y,z)·(- ,
, ,0)=-
,0)=- x+
x+ y=0,
y=0,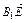 =(x,y,z)·(0,-
=(x,y,z)·(0,- ,-4)=-
,-4)=- y-4z=0,
y-4z=0,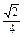 ,∴n="(1,1,-"
,∴n="(1,1,-" 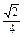 )
)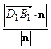 =
=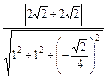 =
=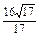 .
.

科目:高中数学 来源:不详 题型:解答题
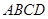 中,
中,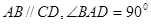 ,
,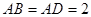 ,
,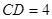 ,点
,点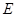 为线段
为线段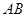 上异于
上异于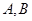 的点,且
的点,且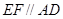 ,沿
,沿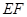 将面
将面 折起,使平面
折起,使平面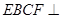 平面
平面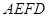 ,如图2.
,如图2.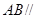 平面
平面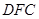 ;
;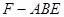 体积最大时,求平面
体积最大时,求平面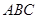 与平面
与平面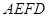 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.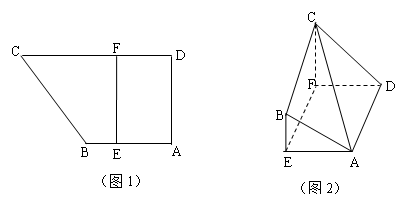
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
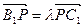 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求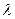 的值.
的值.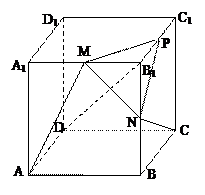
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
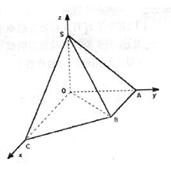
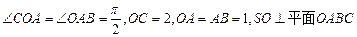 ,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
,SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.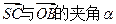 的大小(用反三角函数表示);
的大小(用反三角函数表示);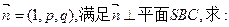
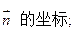
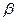 (用反三角函数表示);
(用反三角函数表示);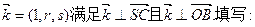
 .
. 
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
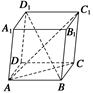
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
类比此性质,如下图,在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,则得到的正确结论为__________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com