
【题目】已知函数![]() 图象中两相邻的最高点和最低点分别为
图象中两相邻的最高点和最低点分别为![]()
![]() ,则函数
,则函数![]() 的单调递增区间为________ ,将函数
的单调递增区间为________ ,将函数![]() 的图象至少平移 ______个单位长度后关于直线
的图象至少平移 ______个单位长度后关于直线![]() 对称.
对称.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识,高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人,女生200人;文科班有男生100人,女生300人.现按男、女用分层抽样从理科生中抽取6人,按男、女分层抽样从文科生中抽取4人,组成环境保护兴趣小组,再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.
(1)设事件![]() 为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件
为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示抽取的4人中文科女生的人数,求
表示抽取的4人中文科女生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
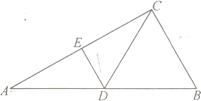
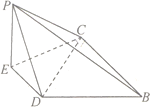
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的准线与椭圆交于
的准线与椭圆交于![]() 两点,过线段
两点,过线段![]() 上的动点
上的动点![]() 作斜率为正的直线
作斜率为正的直线![]() 与抛物线相切,且交椭圆于
与抛物线相切,且交椭圆于![]() 两点.
两点.
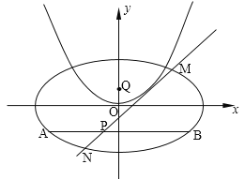
(Ⅰ)求线段![]() 的长及直线
的长及直线![]() 斜率的取值范围;
斜率的取值范围;
(Ⅱ)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为0.设
的公差不为0.设![]() 是数列
是数列![]() 的前
的前![]() 项和.若
项和.若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)是否存在常数![]() ,使得
,使得 为等差数列?并说明理由.
为等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下述结论中错误的是( )
,则下述结论中错误的是( )
A.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 有且仅有
有且仅有![]() 个极小值点
个极小值点
B.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 在
在![]() 上单调递增
上单调递增
C.若![]() 在
在![]() 有且仅有
有且仅有![]() 个零点,则
个零点,则![]() 的范围是
的范围是![]()
D.若![]() 图像关于
图像关于![]() 对称,且在
对称,且在![]() 单调,则
单调,则![]() 的最大值为
的最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com