
【题目】为了估计某校某次数学考试的情况,现从该校参加考试的600名学生中随机抽出60名学生,其数学成绩(百分制)均在![]() 内,将这些成绩分成六组
内,将这些成绩分成六组![]() …
…![]() ,得到如图所示的部分频率分布直方图.
,得到如图所示的部分频率分布直方图.

(1)求抽出的60名学生中数学成绩在![]() 内的人数;
内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校参加考试的学生数学成绩为优秀的人数;
(3)试估计抽出的60名学生的数学成绩的中位数.
【答案】(1)15;(2)135;(3)76.
【解析】
(1)根据频率的和等于1求出成绩在[70,80)内的频率,计算对应的频数即可;
(2)计算不小于85分的频数即可;
(3)根据中位数平分频率分布直方图的面积,求出即可.
(1)在频率分直方图中,小矩形的面积等于这一组的频率,频率的和等于1,
成绩在[70,80)内的频率1﹣(0.005+0.01+0.02+0.035+0.005)×10=0.25.
人数为0.25×60=15人;
(2)估计该校的优秀人数为不小于85分的频率再乘以样本总量600,即
600×(![]() 0.005)×10=135人;
0.005)×10=135人;
(3)分数在[70,80)内的频率为0.25,
∵分数在[40,70)内的频率为:(0.005+0.010+0.020)×10=0.35<0.5,
∴中位数在(70,80]内,
∵中位数要平分直方图的面积,
∴中位数为:70![]() 76.
76.


科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作为加班拍档、创业伴侣、春运神器,曾几何时,方便面是我们生活中重要的“朋友”,然而这种景象却在近![]() 年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续
年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续![]() 年保持两位数增长,2013年的年销量更是创下
年保持两位数增长,2013年的年销量更是创下![]() 亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩
亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩![]() 亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
全国方便面销量情况(单位“亿包/桶)(数据来源:世界方便面协会)
年份 |
|
|
|
|
时间代号 |
|
|
|
|
年销量 |
|
|
|
|
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2017 年(
.用所求回归方程预测2017 年(![]() )方便面在中国的年销量;
)方便面在中国的年销量;
(2)方便面销量遭遇滑铁卢受到哪些因素影响? 中国的消费业态发生了怎样的转变? 某媒体记者随机对身边的![]() 位朋友做了一次调查,其中
位朋友做了一次调查,其中![]() 位受访者表示超过
位受访者表示超过![]() 年未吃过方便面,
年未吃过方便面,![]() 位受访者认为方便面是健康食品;而
位受访者认为方便面是健康食品;而![]() 位受访者有过网络订餐的经历,现从这
位受访者有过网络订餐的经历,现从这![]() 人中抽取
人中抽取![]() 人进行深度访谈,记
人进行深度访谈,记![]() 表示随机抽取的
表示随机抽取的![]() 人认为方便面是健康食品的人数,求随机变量
人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
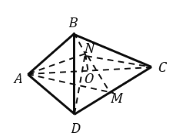
【题目】已知正方形![]() 的边长为
的边长为![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图所示的三棱锥
,得到如图所示的三棱锥![]() ,若
,若![]() 为
为![]() 边的中点,
边的中点,![]() 分别为
分别为![]() 上的动点(不包括端点),且
上的动点(不包括端点),且![]() ,设
,设![]() ,则三棱锥
,则三棱锥![]() 的体积取得最大值时,三棱锥
的体积取得最大值时,三棱锥![]() 的内切球的半径为_______.
的内切球的半径为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛掷一蓝、一黄两枚质地均匀的正四面体骰子,分别观察底面上的数字.

(1)用表格表示试验的所有可能结果;
(2)列举下列事件包含的样本点:A=“两个数字相同”,B=“两个数字之和等于5”,C=“蓝色骰子的数字为2”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com