
 两个项目,投资
两个项目,投资 项目
项目 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:
 项目
项目 万元,一年后获得的利润
万元,一年后获得的利润 (万元)与
(万元)与 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知 项目产品价格在一年内进行
项目产品价格在一年内进行 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
. 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表: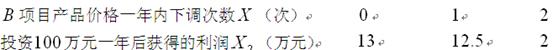
 的方差
的方差 ;
; 的分布列;
的分布列; ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目? ).
).科目:高中数学 来源:不详 题型:解答题
 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从
个白球.已知从 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。 和
和 ;
; 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 的分布列和期望
的分布列和期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
. 的值;
的值; ,求
,求 的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)
的分布列和数学期望.(以直方图中新生上学所需时间少于20分钟的频率作为每名学生上学所需时间少于20分钟的概率)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其他三项挑战失败的概率分别为
,其他三项挑战失败的概率分别为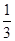 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求随机变量
,求随机变量 的分布列和期望
的分布列和期望 以及方差
以及方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com