练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知数列{an}满足：an=log（n+1）（n+2）定义使a1•a2•…•ak为整数的数k（k∈N*）叫做希望数，则区间[1，2012]内所有希望数的和M=（　　）
    A．2026B．2036C．2046D．2048

    分析 利用an=logn+1（n+2），化简a1•a2•a3…ak，得k=2m-2，给m依次取值，可得区间[1，2012]内所有希望数，然后求和．

    解答 解：an=logn+1（n+2），
    ∴由a1•a2•a3…ak为整数得，log23•log34…log（k+1）（k+2）=log2（k+2）为整数，
    设log2（k+2）=m，则k+2=2m，
    ∴k=2m-2；
    因为211=2048＞2012，
    ∴区间[1，2012]内所有希望数为22-2，23-2，24-2，210-2，
    其和M=22-2+23-2+24-2+…+210-2=2026．
    故选：A

    点评 本题考查对数函数的运算性质，数列求和，求出区间[1，2012]内所有希望数为22-2，23-2，24-2，210-2，是解题的关键

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知AB为⊙O的直径，PH为切线，PE与⊙O交于C、E两点，且与直径AB交于点D，若PH=3$\sqrt{6}$，PC=3$\sqrt{2}$，DE=2$\sqrt{2}$，DB=2．
    （1）求圆O的面积；
    （2）试求线段BE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在极坐标系中，点（2，$\frac{π}{6}$）到直线ρsinθ=3的距离等于2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知点A在函数y=2x的图象上，点B，C在函数y=4•2x的图象上，若△ABC是以B为直角顶点的等腰直角三角形，且点A，C的纵坐标相同，则点B横坐标的值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=sin（$\frac{π}{2}$+x）cosx-sinxcos（3π-x）．
    （1）求函数f（x）的最小正周期；
    （2）在△ABC中，已知A为锐角，f（A）=1，BC=2，B=$\frac{π}{6}$，求AC边的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1（a＞0，b＞0）的一条渐近线方程为y=-2x，则双曲线的实轴长为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{2}$C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知函数f（x）=2x2+3，g（x）=a$\sqrt{{x}^{2}+1}$，若对于任意的x∈R，不等式f（x）＞g（x）恒成立，则实数a的取值范围是（-∞，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

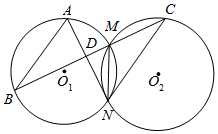    3．如图所示，线段MN是⊙O1和⊙O2的公共弦，AN是⊙O2的切线，过M点的直线分别交⊙O1和⊙O2于B，C两点，交AN于点D．
    （1）证明：$\frac{BD}{CD}$=$\frac{AB}{NC}$；
    （2）若CN是⊙O1的切线，且ND=6，MC=5，AD=2，求CN的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若tan2α=-$\frac{{3\sqrt{7}}}{7}$，α∈（-$\frac{π}{4}$，$\frac{π}{4}}$），则sinα+cosα等于（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{2}$C．$\frac{{\sqrt{5}}}{2}$D．$\frac{{\sqrt{7}}}{2}$

    查看答案和解析>>

    同步练习册答案