
分析 (1)由条件求得m=5,利用二项式系数的性质可得第6项的二项式系数最大,由通项公式可得该项.
(2)设第r+1项的系数的绝对值最大,由通项公式可得C10r210-r≥C10r+129-r,C10r210-r≥C10r-1211-r,求得 r=3,可得第4项的系数的绝对值最大,再利用二项式展开式的通项公式,求得该项.
解答 解:(1)由题意可得22n=2n+992,即(2n-32)(2n+31)=0,∴2n=32,n=5.
由于(2x+$\frac{1}{x}$)10的展开式共有11项,故第6项的二项式系数最大,
由通项公式可得该项为 T6=${C}_{10}^{5}$•(-1)5•25=-8064.
(2)设第r+1项的系数最大,∵Tr+1=${C}_{10}^{r}$•(-1)r•210-r•x10-2r,
∴C10r210-r≥C10r+129-r,C10r210-r≥C10r-1211-r,
求得$\frac{8}{3}$≤r≤$\frac{11}{3}$,∴r=3,
故第4项的系数最大,该项为T4=-C103•27•x4=-15360x4.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:选择题
记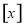 表示不超过
表示不超过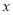 的最大整数,如
的最大整数,如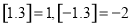 .设函数
.设函数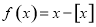 ,若方程
,若方程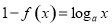 有且仅有3个实数根,则正实数
有且仅有3个实数根,则正实数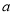 的取值范围为( )
的取值范围为( )
A.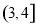 B.
B.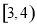 C.
C. D.
D.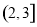
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com