
分析 p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0},则0<a<1;q:函数y=lg(ax2-x+a)的定义域为R,a=0时不成立,a≠0时,则$\left\{\begin{array}{l}{a>0}\\{△=1-4{a}^{2}<0}\end{array}\right.$,解得a范围.如果p∨q为真命题,p∧q为假命题,则命题p与q必然一真一假.
解答 解:p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0},则0<a<1;
q:函数y=lg(ax2-x+a)的定义域为R,a=0时不成立,a≠0时,则$\left\{\begin{array}{l}{a>0}\\{△=1-4{a}^{2}<0}\end{array}\right.$,解得$0<a<\frac{1}{2}$.
如果p∨q为真命题,p∧q为假命题,则命题p与q必然一真一假.
∴$\left\{\begin{array}{l}{0<a<1}\\{a≤0或a≥\frac{1}{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{a≤0或a≥1}\\{0<a<\frac{1}{2}}\end{array}\right.$,
解得$\frac{1}{2}≤a<1$
则实数a的取值范围是.
故答案为:$0<a≤\frac{1}{2}$或a≥1.
点评 本题考查了函数的单调性、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
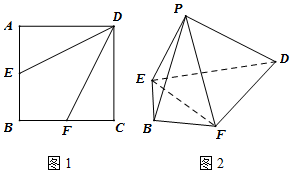 如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.
如图1,边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点P如图2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (-1,6) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
| 频 数 | 15 | 20 | 16 | 31 | 10 | 8 |
| 正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
| 频 数 | 8 | 10 | 20 | 22 | 20 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{2}$,0] | B. | [-π,0] | C. | [-$\frac{π}{4}$,$\frac{π}{4}$] | D. | [0,$\frac{π}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com