
(2011•丰台区二模)已知x,y的取值如下表:从散点图可以看出y与x线性相关,且回归方程为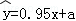 ,则a=( )
,则a=( )
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
A.3.25 B.2.6 C.2.2 D.0
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.3程序框图练习卷(解析版) 题型:?????
(2014•重庆)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )
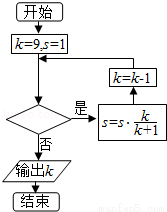
A.s> B.s>
B.s>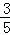 C.s>
C.s>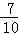 D.s>
D.s>
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 6.2工序流程图练习卷(解析版) 题型:选择题
由如图的流程图输出的s为( )
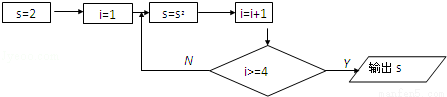
A.64 B.512 C.128 D.256
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 5.1合情推理和演绎推理练习卷(解析版) 题型:?????
(2014•揭阳三模)对于正实数α,Mα为满足下述条件的函数f(x)构成的集合:?x1,x2∈R且x2>x1,有﹣α(x2﹣x1)<f(x2)﹣f(x1)<α(x2﹣x1).下列结论中正确的是( )
A.若f(x)∈Mα1,g(x)Mα2,则f(x)•g(x)∈Mα1•α2
B.若f(x)∈Mα1,g(x)∈Mα2,且g(x)≠0,则
C.若f(x)∈Mα1,g(x)∈Mα2,则f(x)+g(x)∈Mα1+α2
D.若f(x)∈Mα1,g(x)∈Mα2,且α1>α2,则f(x)﹣g(x)∈Mα1﹣α2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.4一元线性回归案例练习卷(解析版) 题型:?????
已知两个相关变量x,y的回归方程是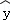 =﹣2x+10,下列说法正确的是( )
=﹣2x+10,下列说法正确的是( )
A.当x的值增加1时,y的值一定减少2
B.当x的值增加1时,y的值大约增加2
C.当x=3时,y的准确值为4
D.当x=3时,y的估计值为4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.4一元线性回归案例练习卷(解析版) 题型:?????
(2014•郑州模拟)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的回归方程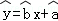 中的
中的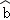 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.4一元线性回归案例练习卷(解析版) 题型:?????
(2014•黄冈模拟)搜集到两个相关变量X,Y的一组数据(xi,yi)(i=1,…,n),经回归分析之后得到回归直线方程中斜率的估计值为2,且 ,则回归直线方程为( )
,则回归直线方程为( )
A.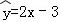 B.
B.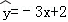 C.
C.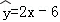 D.
D.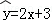
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修1-2 4.3列联表独立性分析案例练习卷(解析版) 题型:?????
(2014•乌鲁木齐一模)若某射击手每次射击击中目标的概率为P(0<P<1),每次射击的结果相互独立,在他连续8次射击中,“恰有3次击中目标”的概率是“恰有5次击中目标”的概率的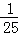 ,则P的值为( )
,则P的值为( )
A. B.
B. C.
C.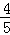 D.
D.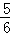
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版必修五 12.2数据表示和特征提取练习卷(解析版) 题型:?????
(2014•广东)已知某地区中小学学生的近视情况分布如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
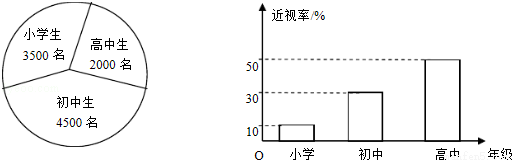
A.200,20 B.100,20 C.200,10 D.100,10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com