
分析 (I)利用复数的运算法则及其有关概念即可得出.
(II)利用双曲线与抛物线的标准方程及其性质即可得出.
解答 (Ι)解:(z1-2)(1+i)=1-i⇒z1=2-i…(2分)
设z2=a+2i,a∈R,则z1z2=(2-i)(a+2i)=(2a+2)+(4-a)i,…(4分)
∵z1z2∈R,∴z2=4+2i…(6分)
(Ⅱ)依题意知$\left\{\begin{array}{l}\frac{b}{a}=\sqrt{3}\\ c=6\\{c^2}={a^2}+{b^2}\end{array}\right.⇒{a^2}=9,{b^2}=27$,-----------(5分)
所以双曲线的方程为$\frac{x^2}{9}-\frac{y^2}{27}=1$-----------------(6分)
点评 本题考查了数的运算法则及其有关概念、双曲线与抛物线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{56}{65}$ | B. | $\frac{56}{65}$ | C. | $-\frac{16}{65}$ | D. | $\frac{16}{65}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
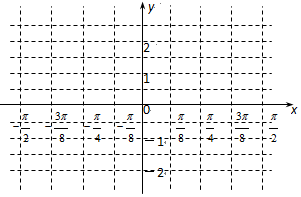 已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.
已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (-2,0) | C. | (0,2) | D. | (0,-2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com