
 某中学进行教学改革试点,推行“高效课堂”的教学方法,为了提高教学效果,某数学教师在甲乙两个平行班进行教学实验,甲班采用传统教学方式,乙班采用“高效课堂”教学方式.为了了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图:记成绩不低于70分者为“成绩优良”
某中学进行教学改革试点,推行“高效课堂”的教学方法,为了提高教学效果,某数学教师在甲乙两个平行班进行教学实验,甲班采用传统教学方式,乙班采用“高效课堂”教学方式.为了了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图:记成绩不低于70分者为“成绩优良”| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(Χ2≤k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据茎叶图计算甲、乙两班数学成绩前10名学生的平均分即可;
(2)填写列联表,计算K2,对照数表即可得出结论.
解答 解:(1)甲班数学成绩前10名学生的平均分为
$\overline{{x}_{甲}}$=$\frac{1}{10}$×(96+80+81+85+89+72+74+74+79+79)=80.9,
乙班数学成绩前10名学生的平均分为
$\overline{{x}_{乙}}$=$\frac{1}{10}$×(93+96+97+99+99+80+81+85+86+78)=89.4;
由此判断使用“高效教学法”的乙班教学效果更佳;
(2)根据茎叶图中的数据,列出列联表,如下;
| 甲班 | 乙班(B方式) | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
点评 本题考查了计算平均数与独立性检验的应用问题,解题时应根据列联表求出观测值,对照临界值表得出结论,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.
某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
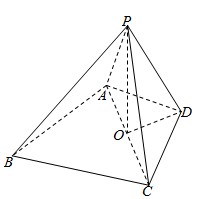 如图四棱锥P-ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1.
如图四棱锥P-ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 474种 | B. | 312种 | C. | 462种 | D. | 300种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{2}$<x<2} | B. | {x|$\frac{1}{2}$<x<1} | C. | {x|-$\frac{1}{2}$<x<1} | D. | {x|-$\frac{1}{2}$<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com