
 某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.
某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.分析 (I)根据面积列出约束条件,作出平面区域;
(II)目标函数为z=2x+3y,即y=-$\frac{2}{3}x$+$\frac{z}{3}$,根据平面区域找到最优解得位置,解方程组得出最优解.
解答 解:(Ⅰ)设工厂用x张甲种薄钢板,y张乙种薄钢板,
则x,y满足的数学关系式为$\left\{\begin{array}{l}{3x+6y≥45}\\{5x+6y≥55}\\{x≥0}\\{y≥0}\end{array}\right.$,
作出二元一次不等式组所表示的平面区域如图所示: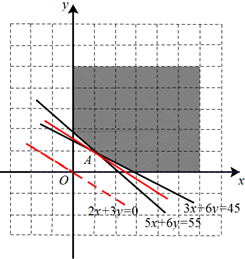
(Ⅱ)设总面积为zm2,则目标函数为:z=2x+3y.
由z=2x+3y得:y=-$\frac{2}{3}x$+$\frac{z}{3}$,
∴由图可知,当直线y=-$\frac{2}{3}x$+$\frac{z}{3}$过点A时,直线的截距最小,即z最小.
解方程组$\left\{\begin{array}{l}{3x+6y=45}\\{5x+6y=55}\end{array}\right.$ 得A(5,5),
∴zmin=2×5+3×5=25.
答:甲,乙两种薄钢板各用5张才能使用料总面积最小,最小面积是25m2.
点评 本题考查了简单线性规划的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
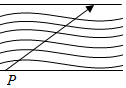 今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$)
今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
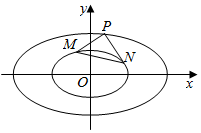 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A($\sqrt{2}$,0),且离心率e=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学进行教学改革试点,推行“高效课堂”的教学方法,为了提高教学效果,某数学教师在甲乙两个平行班进行教学实验,甲班采用传统教学方式,乙班采用“高效课堂”教学方式.为了了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图:记成绩不低于70分者为“成绩优良”
某中学进行教学改革试点,推行“高效课堂”的教学方法,为了提高教学效果,某数学教师在甲乙两个平行班进行教学实验,甲班采用传统教学方式,乙班采用“高效课堂”教学方式.为了了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图:记成绩不低于70分者为“成绩优良”| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(Χ2≤k) | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com