
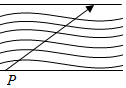
 今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$)
今有一小船位于宽d=60m的河边P处,从这里起,在下游l=80m处河流有一瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为5m/s,如图,为了使小船能安全渡河,船的划速不能小于多少?当划速最小时,划速方向如何?(sin37°=$\frac{3}{5}$) 分析 按向量的平行四边形法则求合速度,即可得出结论.
解答 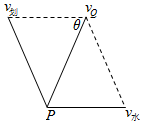
解:如图,由题设可知,船的实际速度$\overrightarrow{v}=\overrightarrow{{v}_{划}}+\overrightarrow{{v}_{水}}$,其方向为临界方向$\overrightarrow{PQ}$,
则最小划速|v划|=|v水|sinθ,sinθ=$\frac{60}{\sqrt{6{0}^{2}+8{0}^{2}}}$=$\frac{3}{5}$,
∴θ=37°.
∴最小划速应为|v划|=|v水|sinθ=3m/s.
点评 解答本题的关键在于运用向量的观点将物理问题转化为数学问题,并建立相应的数学模型,这也将是今后能力培养的主要方面.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
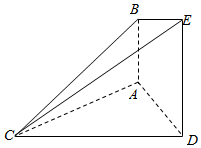 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 据中央电视台新闻联播报道,一周内在某网站下载一次数据,电脑被感染某种病毒的概率是0.65,设在这一周内,某电脑从该网站下载数据n次中被感染这种病毒的次数为X | |
| B. | 某射手射击击中目标的概率为p,设每次射击是相互独立的,从开始射击到击中目标所需要的射击次数为X | |
| C. | 某射手射击击中目标的概率为p,设每次射击是相互独立的,射击n次命中目标的次数为X | |
| D. | 位于某汽车站附近有一个加油站,汽车每次出站后到这个加油站加油的概率为0.6,国庆节这一天有50辆汽车开出该站,假设一天里汽车去该加油站加油是相互独立的,去该加油站加油的汽车数为X |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.
某工厂要制造A种电子装置45台、B种电子装置55台,需用薄钢板给每台装置配一个外壳.已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳均为6个.设工厂用x张甲种薄钢板,y张乙种薄钢板.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
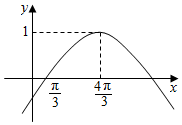
| A. | 2-$\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com